在Rt△ABO中，∠ABO=30°，BO=4，分别以OA、OB边所在的直线建立平面直角坐标系，D为x轴正半轴上一点，以OD为一边在第一象限内作等边△ODE.
（Ⅰ）如图①， 当E点恰好落在线段AB上，求点E的坐标；
（Ⅱ）在（Ⅰ）问的条件下，将△ODE在线段OB上向右平移（如图②），图中是否存在一条与线段
始终相等的线段？如果存在，请指出这条线段，并加以证明；如果不存在，请说明理由.
（Ⅲ）若点D从原点出发沿x轴的正方向移动，设点D到原点的距离为x，△ODE与△AOB重叠部分面积为y，请直接写出y与x的函数关系式，并写出自变量x的取值范围.
已知a、b满足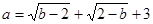
（1）求a、b的值；
（2）求二次函数
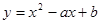图象与x轴交点坐标；（3）写出（2）中，当y>0时，x的取值范围。
如图，△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB与AC、AE分别交于点O、点E，连接EC．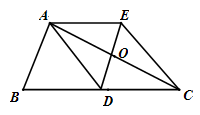
（1）求证：AD=EC；
（2）当∠BAC=90°时，求证：四边形ADCE是菱形；
甲、乙两名同学进行射击训练，在相同条件下各射靶5次，成绩统计如下：
| 命中环数 |
7 |
8 |
9 |
10 |
| 甲命中环数的次数 |
2 |
2 |
0 |
1 |
| 乙命中环数的次 |
1 |
3 |
1 |
0 |
若从甲、乙两人射击成绩方差的角度评价两人的射击水平，则谁的射击成绩更稳定
些？
某班将买一些乒乓球和乒乓球拍，现了解情况如下：甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍．乒乓球拍每副定价30元，乒乓球每盒定价5元．经洽谈后，甲店每买一副球拍赠一盒乒乓球，乙店全部按定价的9折优惠．该班需球拍5副，乒乓球若干盒（不小于5盒）．问：（1）当购买乒乓球多少盒时，两种优惠办法付款一样？
（2）当购买15盒、30盒乒乓球时，请你去办这件事，你打算去哪家商店购买？为什么？