已知函数f(x)=4x3-3x2cosθ+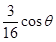 ,其中x∈R,θ为参数,且0≤θ≤2π.
,其中x∈R,θ为参数,且0≤θ≤2π.
(1)当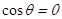 时,判断函数f(x)是否有极值;
时,判断函数f(x)是否有极值;
(2)要使函数f(x)的极小值大于零,求参数θ的取值范围;
(3)若对(2)中所求的取值范围内的任意参数θ,函数f(x)在区间(2A-1,A)内都是增函数,求实数A的取值范围.
已知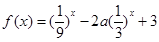

(1)若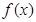 的最小值记为
的最小值记为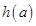 ,求
,求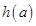 的解析式.
的解析式.
(2)是否存在实数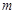 ,
,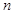 同时满足以下条件:①
同时满足以下条件:①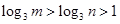 ;②当
;②当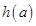 的定义域为[
的定义域为[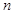 ,
,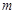 ]时,值域为[
]时,值域为[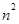 ,
,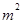 ];若存在,求出
];若存在,求出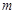 ,
,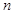 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知函数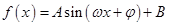 (A>0,ω>0)的一系列对应值如下表:
(A>0,ω>0)的一系列对应值如下表:
| x |
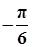 |
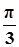 |
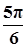 |
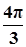 |
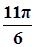 |
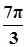 |
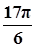 |
| y |
-1 |
1 |
3 |
1 |
-1 |
1 |
3 |
(1)根据表格提供的数据求函数f(x)的一个解析式;
(2)根据(1)的结果,若函数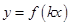 (k>0)周期为
(k>0)周期为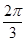 ,当x∈[0,
,当x∈[0,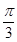 ]时,方程
]时,方程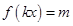 恰有两个不同的解,求实数m的取值范围;
恰有两个不同的解,求实数m的取值范围;
设A>0,A≠1,函数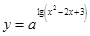 有最大值,
有最大值,
求函数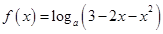 的单调区间.
的单调区间.
若函数y=f(x)在x=x0处取得极大值或极小值,则称x0为函数y=f(x)的极值点.已知A,b是实数,1和-1是函数f(x)=x3+Ax2+b x的两个极值点.
(1)求A和b的值;
(2)设函数g(x)的导函数g′(x)=f(x)+2,求g(x)的极值点.