如图所示,直角梯形ABCD中,AD∥BC,∠B=90°,AD=6,BC=8,AB=3 ,点M是BC的中点,点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动,在点P、Q的运动过程中,以PQ为边作等边△EPQ,使它与梯形ABCD在射线BC的同侧,点P、Q同时出发,点P返回到点M时停止运动,点Q也随之停止,设点P、Q运动的时间是t秒(t>0)。
,点M是BC的中点,点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动,在点P、Q的运动过程中,以PQ为边作等边△EPQ,使它与梯形ABCD在射线BC的同侧,点P、Q同时出发,点P返回到点M时停止运动,点Q也随之停止,设点P、Q运动的时间是t秒(t>0)。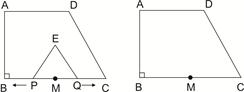
(1)设PQ的长为y,写出y与t之间的函数关系式(写出t的取值范围)。
(2)当BP=1时,求△EPQ与梯形ABCD重叠部分的面积。
(3)随着时间t的变化,线段AD会有一部分被△EPQ覆盖,被覆盖线段的长度在某个时刻会达到最大值,请回答:该最大值能否持续一个时段?若能,直接写出t的取值范围;若不能,请说明理由。
小明所在班组织全部同学参加上海世博园,由于时间原因,每个学生只能在所给的场馆单(如图)上随机选择,选择方式规定为在3个发展中国家馆和4个发达国家馆中分别选一个馆参观。场馆单上的3个发展中国家馆包括:A中国馆、B印度馆、C巴西馆;4个发达国家馆包括:D美国馆、E日本馆、F德国馆、G法国馆,其中中国馆、印度馆、日本馆属于亚洲馆。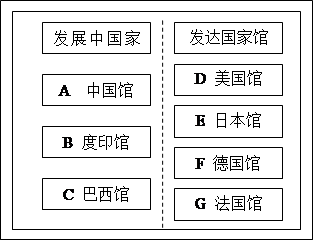
(1)请你用列表或画树状图的方法,分析并写出小明所有可能的参观方式。(馆名用字母表示即可)
(2)求小明所选择参观的两个馆恰好都是亚洲馆的概率。
如图,在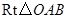 中,
中,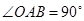 ,且点
,且点 的坐标为(4,2).
的坐标为(4,2).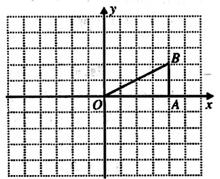
(1)画出 绕点
绕点 逆时针旋转
逆时针旋转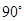 后的
后的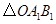 ;
;
(2)求点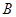 旋转到点
旋转到点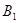 所经过的路线长.
所经过的路线长.
解方程: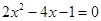
已知抛物线的顶点(-1,-4)且过点(0,-3),直线l是它的对称轴。
(1)求此抛物线的解析式;
(2)设抛物线交x轴于点A、B(A在B的左边),交y轴于点C,P为l上的一动点,当△PBC的周长最小时,求P点的坐标。
(3)在直线l上是否存在点M,使△MBC是等腰三角形,若存在,直接写出符合条件的点M的坐标;若不存在请说明理由。
在数学学习和研究中经常需要总结运用数学思想方法。如类比、转化、从特殊到一般等思想方法,如下是一个案例,请补充完整。
题目:如图1,在平行四边形ABCD中,点E是BC的中点,点F在线段AE上,BF的延长线交射线CD于点G,若 ,求
,求 的值。
的值。
(1)尝试探究
在图1中,过点E作EH∥AB交BG于点H,则易求 的值是,
的值是, 的值是
的值是
,从而确定 的值是。
的值是。
(2)类比延伸
如图2,在原题的条件下,若 ,则
,则 的值是。(用含m的代数式表示),写出解答过程。
的值是。(用含m的代数式表示),写出解答过程。
(3)拓展迁移
如图3,在梯形ABCD中,DC∥AB,点E是BC延长线上的一点,AE和BD相交于F,若 ,
, (a>0,b>0),则
(a>0,b>0),则 的值是。(用含a、b的代数式表示)写出解答过程。
的值是。(用含a、b的代数式表示)写出解答过程。