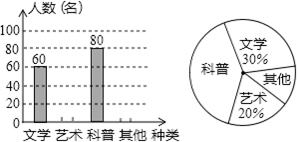某校为开展每天一小时阳光体育活动,准备组建篮球、排球、足球、乒乓球四个兴趣小组,并规定每名学生至少参加1个小组,也可兼报多个小组.该校对八年级全体学生报名情况进行了抽样调查,并将所得数据制成如下两幅统计图:
根据图中的信息解答下列问题:
(1)补全条形统计图;
(2)若该校八年级共有400名学生,估计报名参加2个兴趣小组的人数;
(3)综合上述信息,谈谈你对该校即将开展的兴趣小组活动的意见和建议.(字数不超过30字)
某学校抽查了某班级某月10天的用电量,数据如下表(单位:度);
| 度数 |
8 |
9 |
10 |
13 |
14 |
15 |
| 天数 |
1 |
1 |
2 |
3 |
1 |
2 |
(1)这10天用电量的众数是_______,中位数是_______,极差是_______;
(2)求这个班级平均每天的用电量;
(3)已知该校共有20个班级,该月共计30天,试估计该校该月总的用电量.
学习成为商城人的时尚,义乌市新图书馆的启用,吸引了大批读者.有关部门统计了2011年10月至2012年3月期间到市图书馆的读者的职业分布情况,统计图如下:
(1)在统计的这段时间内,共有_______万人到市图书馆阅读,其中商人所占百分比是_______,并将条形统计图补充完整(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑);
(2)若今年4月到市图书馆的读者共28000名,估计其中约有多少名职工?
某校对九年级500名同学完成数学学习任务情况进行随机抽查,抽查结果分为“很好”、“较好”、“一般”、“较差”四个等级.根据抽查的数据,制成不完整的表格和扇形统计图如下:
| 完成情况 |
很好 |
较好 |
一般 |
较差 |
| 人数 |
30 |
45 |
a |
15 |
根据所学知识分析,解答下列问题:
(1)补填表图中的空缺:a=_______,m=_______,n=_______.
(2)通过计算,估计全校完成学习任务(一般、较好、很好)的同学有多少人?
(3)请你根据自己的知识和经验,或者从数据分析角度,给某等级的同学提些合理化的建议,目标或给予评价.
某校为了解学生的课外阅读情况,就“我最喜爱的课外读物”对文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),并根据调查结果绘制了两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)这次被调查的学生共有多少名?
(2)请将条形统计图补充完整;并在扇形统计图中,计算出“其他类”所对应的圆心角的度数;
(3)若该校有2400名学生,请你估计该校喜爱“科普类”的学生有多少名.