(算一算)
如图 ① ,点 A 、 B 、 C 在数轴上, B 为 AC 的中点,点 A 表示 ,点 B 表示 1 ,则点 C 表示的数为 , AC 长等于 ;
(找一找)
如图②,点 M 、 N 、 P 、 Q 中的一点是数轴的原点,点 A 、 B 分别表示实数 、 , Q 是 AB 的中点,则点 是这个数轴的原点;
(画一画)
如图 ③ ,点 A 、 B 分别表示实数 、 ,在这个数轴上作出表示实数 n 的点 E (要求:尺规作图,不写作法,保留作图痕迹);
(用一用)
学校设置了若干个测温通道,学生进校都应测量体温,已知每个测温通道每分钟可检测 a 个学生.凌老师提出了这样的问题:假设现在校门口有 m 个学生,每分钟又有 b 个学生到达校门口.如果开放 3 个通道,那么用 4 分钟可使校门口的学生全部进校;如果开放 4 个通道,那么用 2 分钟可使校门口的学生全部进校.在这些条件下, a 、 m 、 b 会有怎样的数量关系呢?
爱思考的小华想到了数轴,如图 ④ ,他将 4 分钟内需要进校的人数 记作 ,用点 A 表示;将 2 分钟内由 4 个开放通道检测后进校的人数,即校门口减少的人数 记作 ,用点 B 表示.
① 用圆规在小华画的数轴上分别画出表示 、 的点 F 、 G ,并写出 的实际意义;
② 写出 a 、 m 的数量关系: .
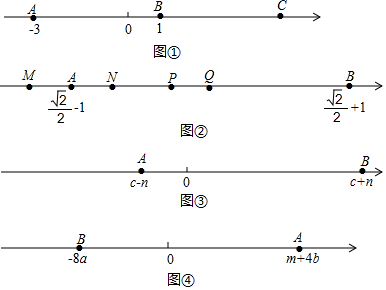
如图,在平面直角坐标系中,点 为坐标原点,抛物线 的顶点是 ,将 绕点 顺时针旋转 后得到 ,点 恰好在抛物线上, 与抛物线的对称轴交于点 .
(1)求抛物线的解析式;
(2) 是线段 上一动点,且不与点 , 重合,过点 作平行于 轴的直线,与 的边分别交于 , 两点,将 以直线 为对称轴翻折,得到△ ,设点 的纵坐标为 .
①当△ 在 内部时,求 的取值范围;
②是否存在点 ,使 ,若存在,求出满足条件 的值;若不存在,请说明理由.
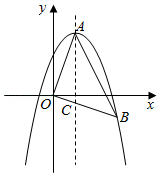
如图,在 中, 为 的直径, 为 上一点, 是 的中点,过点 作 的垂线,交 的延长线于点 ,连接 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

某超市销售 、 两款保温杯,已知 款保温杯的销售单价比 款保温杯多10元,用480元购买 款保温杯的数量与用360元购买 款保温杯的数量相同.
(1) 、 两款保温杯的销售单价各是多少元?
(2)由于需求量大, 、 两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且 款保温杯的数量不少于 款保温杯数量的两倍.若 款保温杯的销售单价不变, 款保温杯的销售单价降低 ,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?
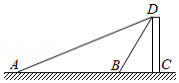
如图,为测量建筑物 的高度,在 点测得建筑物顶部 点的仰角为 ,再向建筑物 前进30米到达 点,测得建筑物顶部 点的仰角为 , , 三点在一条直线上),求建筑物 的高度.(结果保留整数.参考数据: , , , , ,
为了解某校九年级学生的体质健康状况,随机抽取了该校九年级学生的 进行测试,将这些学生的测试成绩 分为四个等级:优秀 ;良好 ;及格 ;不及格 ,并绘制成如图两幅统计图.
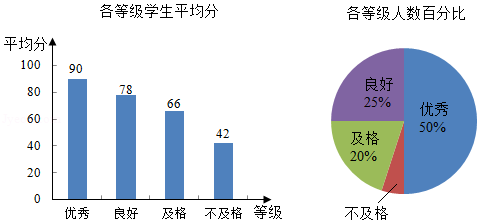
根据以上信息,解答下列问题:
(1)在抽取的学生中不及格人数所占的百分比是 ;
(2)计算所抽取学生测试成绩的平均分;
(3)若不及格学生的人数为2人,请估算出该校九年级学生中优秀等级的人数.