设
是如下形式的2行3列的数表,
满足性质 ,且
记
为
的第
行各数之和(
=1,2),
为
的第
列各数之和(
=1,2,3)记
为
中的最小值。
(1)对如下表
,求
的值
| 1 |
1 |
|
(2)设数表 形如
| 1 |
1 |
|
| - |
其中
,求
的最大值
(3)对所有满足性质P的2行3列的数表
,求
的最大值。
抛物线C的顶点为坐标原点O.焦点在x轴上,直线l: 交C于P,Q两点,且 .已知点 ,且 与l相切.
(1)求C, 的方程;
(2)设 是C上的三个点,直线 , 均与 相切.判断直线 与 的位置关系,并说明理由.
设函数 ,其中 .
(1)讨论 的单调性;
(2)若 的图像与
轴没有公共点,求a的取值范围.
的图像与
轴没有公共点,求a的取值范围.
已知直三棱柱
中,侧面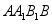 为正方形,
,E,F分别为
和
的中点,
.
为正方形,
,E,F分别为
和
的中点,
.

(1)求三棱锥 的体积;
(2)已知D为棱 上的点,证明: .
记 为数列 的前n项和,已知 ,且数列 是等差数列,证明: 是等差数列.
甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表:
|
一级品 |
二级品 |
合计 |
|
|
甲机床 |
150 |
50 |
200 |
|
乙机床 |
120 |
80 |
200 |
|
合计 |
270 |
130 |
400 |
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?
(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?
附:
|
|
0.050 |
0.010 |
0.001 |
|
k |
3.841 |
6.635 |
10.828 |