经英国相关机构判断,MH370在南印度洋海域消失.中国两舰艇随即在边长为100海里的某正方形ABCD(如图)海域内展开搜索.两艘搜救船在A处同时出发,沿直线AP、AQ向前联合搜索,且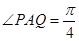 (其中点P、Q分别在边BC、CD上),搜索区域为平面四边形APCQ围成的海平面.设
(其中点P、Q分别在边BC、CD上),搜索区域为平面四边形APCQ围成的海平面.设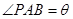 ,搜索区域的面积为
,搜索区域的面积为 .
.
(1)试建立 与
与 的关系式,并指出
的关系式,并指出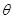 的取值范围;
的取值范围;
(2)求 的最大值,并求此时
的最大值,并求此时 的值.
的值.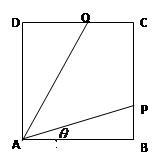
已知方程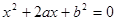 是关于
是关于 的一元二次方程.
的一元二次方程.
(1)若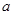 是从集合
是从集合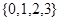 四个数中任取的一个数,
四个数中任取的一个数, 是从集合
是从集合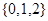 三个数中任取的一个数,求上述方程有实数根的概率;
三个数中任取的一个数,求上述方程有实数根的概率;
(2)若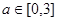 ,
, ,求上述方程有实数根的概率.
,求上述方程有实数根的概率.
已知 ,
,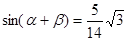 ,
, ,
, ,求
,求 的值.
的值.
如图所示,在 中,
中, ,
, ,
, ,求
,求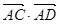 的值.
的值.
假定下述数据是甲、乙两个供货商的交货天数:
甲:10 9 10 10 11 11 9 11 10 10
乙:8 10 14 7 10 11 10 8 15 12
估计两个供货商的交货情况,并问哪个供货商交货时间短一些,哪个供货商交货时间较具一致性与可靠性.