设
,证明:
(Ⅰ)当
时,
;
(Ⅱ)当
时,
。
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=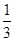 BB1,C1F=
BB1,C1F=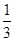 CC1.
CC1.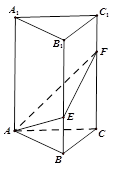
(1)求异面直线AE与A1 F所成角的大小;
(2)求平面AEF与平面ABC所成角的余弦值.
设x,y均为正数,且x>y,求证:2x+ ≥2y+3.
≥2y+3.
在平面直角坐标系xOy中,直线m的参数方程为 (t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsin2θ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长.
(t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsin2θ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长.
已知M= ,N=
,N= ,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程.
,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程.
如图,已知AB为圆O的直径,BC切圆O于点B,AC交圆O于点P,E为线段BC的中点.求证:OP⊥PE.