小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.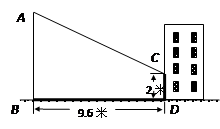
如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=2,CD平行于AB,并与弧AB相交于点M、N.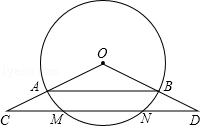
(1)求线段OD的长;
(2)若tan∠C=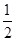 ,求弦MN的长.
,求弦MN的长.
如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=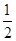 ∠CAB.
∠CAB.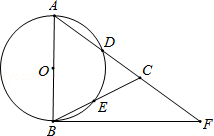
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=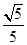 ,求BC和BF的长.
,求BC和BF的长.
如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.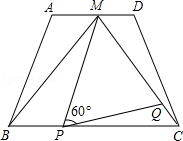
(1)求证:梯形ABCD是等腰梯形;
(2)动点P、Q分别在线段BC和MC上运动,且∠MPQ=60°保持不变.设PC=x,MQ=y,求y与x的函数关系式;
(3)在(2)中:
①当动点P、Q运动到何处时,以点P、M和点A、B、C、D中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;
②当y取最小值时,判断△PQC的形状,并说明理由.
已知抛物线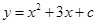 过两点(m,0)、(n,0),且
过两点(m,0)、(n,0),且 ,抛物线于双曲线
,抛物线于双曲线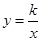 (x>0)的交点为(1,d).
(x>0)的交点为(1,d).
(1)求抛物线与双曲线的解析式;
(2)已知点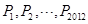 都在双曲线
都在双曲线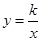 (x>0)上,它们的横坐标分别为
(x>0)上,它们的横坐标分别为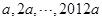 ,O为坐标原点,记
,O为坐标原点,记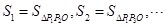 ,点Q在双曲线
,点Q在双曲线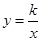 (x<0)上,过Q作QM⊥y轴于M,记
(x<0)上,过Q作QM⊥y轴于M,记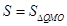 。
。
求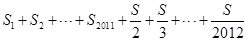 的值.
的值.
做服装生意的王老板经营甲、乙两个店铺,每个店铺在同一段时间内都能售出A,B两种款式的服装合计30件,并且每售出一件A款式和B款式服装,甲店铺获毛利润分别为30元和40元,乙店铺获毛利润分别为27元和36元。某日王老板进货A款式服装35件,B款式服装25件。怎样分配给每个店铺各30件服装,使得在保证乙店铺毛利润不小于950元的前提下,王老板获取的总毛利润最大?最大的总毛利润是多少?