操作:如图,在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角板的直角顶点与点P重合,并且一条直角边始终经过点B,另一直角边与正方形的某一边所在直线交于点E.
探究:①观察操作结果,哪一个三角形与△BPC相似,写出你的结论,(找出两对即可);并选择其中一组说明理由;
②当点P位于CD的中点时,直接写出① 中找到的两对相似三角形的相似比和面积比.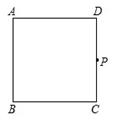
如图,A.B两个转盘分别被分成三个、四个相同的扇形,分别转动A盘、B盘各一次(若指针恰好指在分割线上,则重转一次,直到指针指向一个数字为止).
(1) 如图1,两个指针所指的区域内的数字之和大于7的概率为_________;
(2) 如果将图1中的转盘改为图2,其余不变,用列表或画树状图的方法,求两个指针所知区域的数字之和大于7 的概率.
如图,在△ABC中,BC=12cm,AB=AC, ∠BAC=120°.
(1)尺规作图:作△ABC的外接圆(只需作出图形,并保留作图痕迹);
(2)求它的外接圆半径.
已知二次函数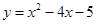
(1)求函数图象的顶点坐标、对称轴及与坐标轴的交点坐标,并画出函数的大致图象;
(2)由图象可知,当x取何值时, ?
?
已知Rt△ABC中,AC=BC=2.一直角的顶点P在AB上滑动,直角的两边分别交线段AC,BC于E.F两点
(1)如图1,当 且PE⊥AC时,求证:
且PE⊥AC时,求证: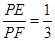 ;
;
(2)如图2,当 时(1)的结论是否仍然成立?为什么?
时(1)的结论是否仍然成立?为什么?
(3)在(2)的条件下,将直角∠EPF绕点P旋转,设∠BPF=α(0°<α<90°).连结EF,当△CEF的周长等于2+ 时,请直接写出α的度数.
时,请直接写出α的度数.
如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从B出发沿BA向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点,点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm,当点Q到达顶点C时,P,Q同时停止运动,设P,Q两点运动时间为t秒.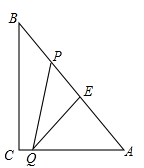
(1)当t为何值时,PQ∥BC?
(2)设四边形PQCB的面积为y,求y关于t的函数关系式;并说明四边形PQCB面积能否是△ABC面积的 ?若能,求出此时t的值;若不能,请说明理由;
?若能,求出此时t的值;若不能,请说明理由;
(3)当t为何值时,△AEQ为等腰三角形?(直接写出结果)