已知,如图, 是以线段
是以线段 为直径的
为直径的 的切线,
的切线, 交
交 于点
于点 ,过点
,过点 作弦
作弦 垂足为点
垂足为点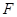 ,连接
,连接 .
.
(1)仔细观察图形并写出四个不同的正确结论:①________,②________ ,③________,④____________(不添加其它字母和辅助线,不必证明);
(2) =
= ,
, =
=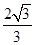 ,求
,求 的半径
的半径
某超市拟于中秋节前50天里销售某品牌月饼,其进价为18元 .设第 天的销售价格为 (元 ,销售量为 .该超市根据以往的销售经验得出以下的销售规律:①当 时, ;当 时, 与 满足一次函数关系,且当 时, ; 时, .② 与 的关系为 .
(1)当 时, 与 的关系式为 ;
(2) 为多少时,当天的销售利润 (元 最大?最大利润为多少?
(3)若超市希望第31天到第35天的日销售利润 (元 随 的增大而增大,则需要在当天销售价格的基础上涨 元 ,求 的取值范围.
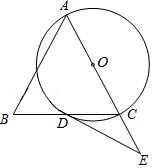
如图, 中, ,以 为直径的 交 于点 ,点 为 延长线上一点,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径.
已知关于 的一元二次方程 有两个不相等的实数根 , .
(1)求 的取值范围;
(2)若 ,且 为整数,求 的值.
第一盒中有2个白球、1个黄球,第二盒中有1个白球、1个黄球,这些球除颜色外无其他差别.
(1)若从第一盒中随机取出1个球,则取出的球是白球的概率是 .
(2)若分别从每个盒中随机取出1个球,请用列表或画树状图的方法求取出的两个球中恰好1个白球、1个黄球的概率.
如图,拦水坝的横断面为梯形 , ,坝高 ,坡角 , ,求 的长.
