(本小题满分13分)
如图,已知四棱柱ABCD—A1B1C1D1中,A1D⊥底面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2。
(I)求证:C1D//平面ABB1A1;
(II)求直线BD1与平面A1C1D所成角的正弦值;
(Ⅲ)求二面角D—A1C1—A的余弦值。
(本小题满分13分)
一个盒子中装有5张卡片,每张卡片上写有一个数字,数字分别是1、2、3、5,现从盒子中随机抽取卡片。
(I)若从盒子中有 放回地抽取3次卡片,每次抽取一张,求恰有两次取到的卡片上数字为偶数的概率;
放回地抽取3次卡片,每次抽取一张,求恰有两次取到的卡片上数字为偶数的概率;
(II)若从盒子中依次抽取卡片,每次抽取一张,取出的卡片不放回,当取到一张记有偶数的卡片即停止抽取,否则继续抽取卡片,求抽取次数X的分布列和期望。
(本小题满分13分)
如图,在四边形ABCD中,AB=3,AD=BC=CD=2,A=60°。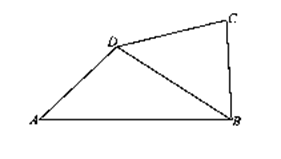
(1)求 的值;
的值;
(2)求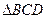 的面积。
的面积。

(本小题满分12分)
如图,在正方体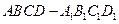 中,
中,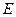 、
、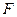 分别是
分别是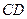 、
、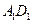 中点
中点
(1)求证: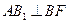 ;
;
(2)求证: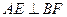 ;
;
(3)棱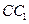 上是否存在点
上是否存在点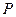 ,使
,使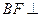 平面
平面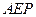 ,若存在,确定点
,若存在,确定点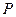 位置;若不存在,说明理由.
位置;若不存在,说明理由.
(本小题满分12分)
网站就观众对某小品类节目的喜爱程度进行网上调查,其中持各种态度的人数如下表:
| 喜欢 |
一般 |
不喜欢 |
|
| 人数 |
560 |
240 |
200 |
(1)现用分层抽样的方法从所有参与网上调查的观众中抽取了一个容量为 的样本,已知从不喜欢小品的观众中国抽取的人数为5人,则
的样本,已知从不喜欢小品的观众中国抽取的人数为5人,则 的值为多少?
的值为多少?
(2)在(1)的条件下,若抽取到的5名不喜欢小品的观众中有2名女性,现将抽取到的5名不喜欢小品的观众看成一个总体,从中任取两名观众,求至少有一名为女性观众的概率.