(本小题满分12分)已知 ,函数
,函数 ,
, .
.
(1)若曲线 与曲线
与曲线 在它们的交点
在它们的交点 处的切线重合,求
处的切线重合,求 ,
, 的值;
的值;
(2)设 ,若对任意的
,若对任意的 ,且
,且 ,都有
,都有 ,求
,求 的取值范围.
的取值范围.
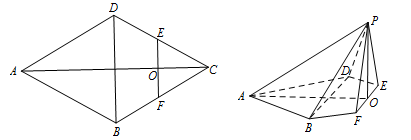
如图,在边长为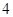 的菱形
的菱形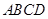 中,
中,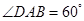 ,点
,点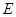 ,
,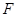 分别是边
分别是边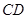 ,
,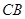 的中点,
的中点,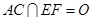 ,沿
,沿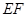 将△
将△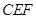 翻折到△
翻折到△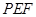 ,连接
,连接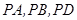 ,得到如图的五棱锥
,得到如图的五棱锥 ,且
,且 .
.
(1)求证: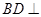 平面
平面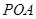 ;
;
(2)求二面角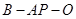 的正切值.
的正切值.
为了解甲、乙两厂的产品质量,分别从两厂生产的产品中各随机抽取10件,测量产品中某种元素的含量(单位:毫克),其测量数据的茎叶图如下: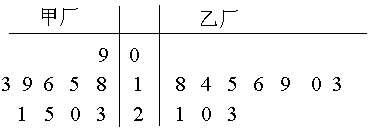
规定:当产品中此种元素含量大于18毫克时,认定该产品为优等品。
(1)试比较甲、乙两厂生产的产品中该种元素含量的平均值的大小;
(2)从乙厂抽出上述10件产品中,随机抽取3件,求抽到的3件产品中优等品数 的分布列及数学期望。
的分布列及数学期望。
某同学用“五点法”画函数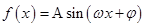 在某一个周期的图象时,列表并填入的部分数据如下表:
在某一个周期的图象时,列表并填入的部分数据如下表: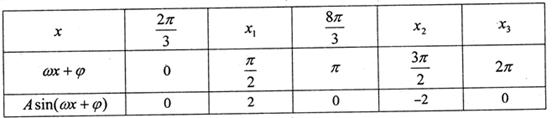
(1)求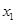 ,
,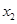 ,
,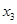 的值及函数
的值及函数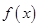 的表达式;
的表达式;
(2)将函数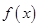 的图象向左平移
的图象向左平移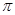 个单位,可得到函数
个单位,可得到函数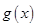 的图象,求函数
的图象,求函数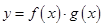 在区间
在区间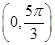 的最小值.
的最小值.
小王在某社交网络的朋友圈中,向在线的甲、乙、丙随机发放红包,每次发放1个.
(Ⅰ)若小王发放5元的红包2个,求甲恰得1个的概率;
(Ⅱ)若小王发放3个红包,其中5元的2个,10元的1个.记乙所得红包的总钱数为X,求X的分布列和期望.
已知函数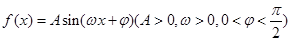 部分图象如图所示。
部分图象如图所示。
(1)求函数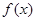 的解析式;
的解析式;
(2)当 时,求函数
时,求函数 的值域。
的值域。