四边形一条对角线所在直线上的点，如果到这条对角线的两端点的距-优题课

四边形一条对角线所在直线上的点，如果到这条对角线的两端点的距离不相等，但到另一对角线的两个端点的距离相等，则称这点为这个四边形的准等距点．如右图，点P为四边形ABCD对角线AC所在直线上的一点，PD=PB，PA≠PC，则点P为四边形ABCD的准等距点．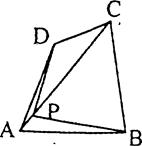

(1)如图2，画出菱形ABCD的一个准等距点．
(2)如图3，作出四边形ABCD的一个准等距点(尺规作图，保留作
图痕迹不要求写作法)．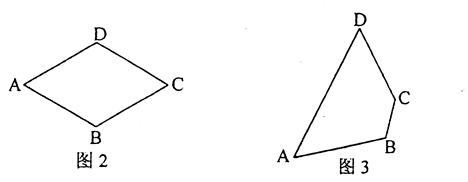

科目数学题型解答题难度中等

知识点：圆内接四边形的性质

某校在七、八、九三个年级中进行“一带一路”知识竞赛，分别设有一等奖、二等奖、三等奖、优秀奖、纪念奖．现对三个年级同学的获奖情况进行了统计，其中获得纪念奖有17人，获得三等奖有10人，并制作了如图不完整的统计图．

（1）求三个年级获奖总人数；

（2）请补全扇形统计图的数据；

（3）在获一等奖的同学中，七年级和八年级的人数各占 $\frac{1}{4}$ ，其余为九年级的同学，现从获一等奖的同学中选2名参加市级比赛，通过列表或者树状图的方法，求所选出的2人中既有七年级又有九年级同学的概率．

如图， $AB = AD$ ， $AC = AE$ ， $∠ BAE = ∠ DAC$ ．求证： $∠ C = ∠ E$ ．

（1）计算： ${(2019 - \sqrt{2})}^{0} - 2^{- 1} + | - 1 | + \sin^{2} 45 °$

（2）化简： $\frac{2 xy}{x^{2} - y^{2}} \div (\frac{1}{x - y} + \frac{1}{x + y})$

已知二次函数 $y = a x^{2} (a \neq 0)$ 的图象过点 $(2, - 1)$ ，点 $P (P$ 与 $O$ 不重合）是图象上的一点，直线 $l$ 过点 $(0, 1)$ 且平行于 $x$ 轴． $PM ⊥ l$ 于点 $M$ ，点 $F (0, - 1)$ ．

（1）求二次函数的解析式；

（2）求证：点 $P$ 在线段 $MF$ 的中垂线上；

（3）设直线 $PF$ 交二次函数的图象于另一点 $Q$ ， $QN ⊥ l$ 于点 $N$ ，线段 $MF$ 的中垂线交 $l$ 于点 $R$ ，求 $\frac{MR}{RN}$ 的值；

（4）试判断点 $R$ 与以线段 $PQ$ 为直径的圆的位置关系．

如图，已知 $AB$ 是 $⊙ O$ 的直径， $AC$ ， $BC$ 是 $⊙ O$ 的弦， $OE / / AC$ 交 $BC$ 于 $E$ ，过点 $B$ 作 $⊙ O$ 的切线交 $OE$ 的延长线于点 $D$ ，连接 $DC$ 并延长交 $BA$ 的延长线于点 $F$ ．

（1）求证： $DC$ 是 $⊙ O$ 的切线；

（2）若 $∠ ABC = 30 °$ ， $AB = 8$ ，求线段 $CF$ 的长．

试卷网试题网古诗词网作文网范文网