(10分)在一次国际大型体育运动会上,某运动员报名参加了其中5个项目的比赛.已知该运动员在这5个项目中,每个项目能打破世界纪录的概率都是0.8,那么在本次运动会上:
(1)求该运动员至少能打破3项世界纪录的概率;
(2)若该运动员能打破世界纪录的项目数为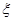 ,求
,求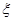 的数学期望
的数学期望 (即均值).
(即均值).
△ABC的三个内角A、B、C的对边的长分别为 a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1)
a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1)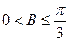 ;(2)
;(2)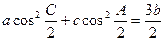 ;(3)
;(3)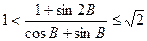 。
。
请你选取给定的两个条件中的一个条件为条件,三个结论中的两个为结论,组建一个你认为正确的命题,并证明之。
(I)组建的命题为:已知_______________________________________________
求证:①_________________ _______
_______ __________________
__________________
②__________________________________________ (II)证明:
(II)证明:
2010年4月14日清晨我国青海省玉树县发生里氏7.1级强震。国家抗 震救灾指挥部迅速成立并调拨一批救灾物资从距离玉树县400千米的某地A运往玉树县,这批救灾物资随17辆车以
震救灾指挥部迅速成立并调拨一批救灾物资从距离玉树县400千米的某地A运往玉树县,这批救灾物资随17辆车以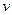 千米/小时的速度匀速直达灾区,为了安全起见,每两辆车之间的间距不得小于
千米/小时的速度匀速直达灾区,为了安全起见,每两辆车之间的间距不得小于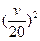 千米。设这批救灾物资全部运送到灾区(不考虑车辆的长度)所需要的时间为
千米。设这批救灾物资全部运送到灾区(不考虑车辆的长度)所需要的时间为 小时。求这批救灾物资全部运送到灾区所需要的最短时间,并指出此时车辆行驶的速度。
小时。求这批救灾物资全部运送到灾区所需要的最短时间,并指出此时车辆行驶的速度。
如图,在四边形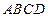 中,
中, ,
, ,
, ,
, ,
,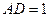 ,求四边形
,求四边形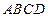 绕
绕 旋转一周所成几何体的表面积及体积。
旋转一周所成几何体的表面积及体积。
已知 为等比数列,
为等比数列, ,求
,求 的通项公式
的通项公式 。
。
已知点(1, )是函数
)是函数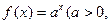 且
且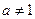 )的图象上一点,等比数列
)的图象上一点,等比数列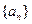 的前n项和为
的前n项和为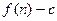 ,数列
,数列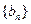
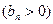 的首项为c,且前n项和
的首项为c,且前n项和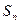 满足
满足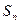 -
-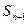 =
=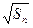 +
+ (n
(n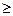 2).
2).
(Ⅰ)求数列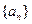 和
和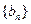 的通项公式;
的通项公式;
(Ⅱ)若数列{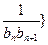 前n项和为
前n项和为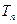 ,问
,问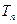 >
> 的最小正整数n是多少?
的最小正整数n是多少?