(本题满分13分)已知数列{an}的前n项和为Sn,且an=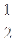 (3n+Sn)对一切正整数n成立
(3n+Sn)对一切正整数n成立
(I)证明:数列{3+an}是等比数列,并求出数列{an}的通项公式;
(II)设 ,求数列
,求数列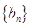 的前n项和Bn;
的前n项和Bn;
a11,a12,……a18
a21,a22,……a28
…………………
a81,a82,……a88
64个正数排成8行8列, 如上所示:在符合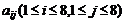 中,i表示该数所在的行数,j表示该数所在的列数。已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且
中,i表示该数所在的行数,j表示该数所在的列数。已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且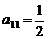 ,
,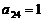 ,
, 。
。
⑴若 ,求
,求 和
和 的值。
的值。
⑵记第n行各项之和为An(1≤n≤8),数列{an}、{bn}、{cn}满足 ,联
,联 (m为非零常数),
(m为非零常数), ,且
,且 ,求
,求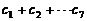 的取值范围。
的取值范围。
⑶对⑵中的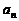 ,记
,记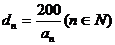 ,设
,设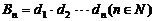 ,求数列
,求数列 中最大项的项数。
中最大项的项数。
若给定椭圆C:ax2+by2=1(a>0,b>0,a b)和点N(x0,y0),则称直线l:ax0x+by0y=1为椭圆C的“伴随直线”,
b)和点N(x0,y0),则称直线l:ax0x+by0y=1为椭圆C的“伴随直线”,
(1)若N(x0,y0)在椭圆C上,判断椭圆C与它的“伴随直线”的位置关系(当直线与椭圆的交点个数为0个、1个、2个时,分别称直线与椭圆相离、相切、相交),并说明理由;
(2)命题:“若点N(x0,y0)在椭圆C的外部,则直线l与椭圆C必相交.”写出这个命题的逆命题,判断此逆命题的真假,说明理由;
(3)若N(x0,y0)在椭圆C的内部,过N点任意作一条直线,交椭圆C于A、B,交l于M点(异于A、B),设 ,
,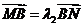 ,问
,问 是否为定值?说明理由.
是否为定值?说明理由.
如图,二面角D—AB—E的大小为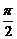 ,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
⑴求证AE⊥平面BCE;
⑵求二面角B—AC—E的正弦值;
⑶求点D到平面ACE的距离.
已知直线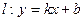 ,曲线
,曲线
(1)若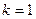 且直线与曲线恰有三个公共点时,求实数
且直线与曲线恰有三个公共点时,求实数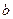 的取值;
的取值;
(2)若 ,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。
,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。
(本小题满分15分)已知函数 。
。
(1)若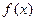 的图象有与
的图象有与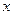 轴平行的切线,求
轴平行的切线,求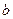 的取值范围;
的取值范围;
(2)若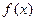 在
在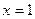 时取得极值,且
时取得极值,且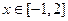 时,
时,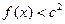 恒成立,求
恒成立,求 的取值范围。
的取值范围。