如图,在四边形ABCD中,对角线AC、BD相交于点O,直线MN经过点O,设锐角∠DOC=∠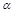 ,将△DOC以直线MN为对称轴翻折得到△D’OC’,直线A D’、B C’相交于点P.
,将△DOC以直线MN为对称轴翻折得到△D’OC’,直线A D’、B C’相交于点P.
(Ⅰ)当四边形ABCD是矩形时,如图1,请猜想A D’、B C’的数量关系以及∠APB与∠α的大小关系;
(Ⅱ)当四边形ABCD是平行四边形时,如图2,(1)中的结论还成立吗?
(Ⅲ)当四边形ABCD是等腰梯形时,如图3,∠APB与∠α有怎样的数量关系?请证明.
如图,将 沿
沿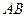 方向平移
方向平移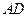 距离得到
距离得到 ,已知
,已知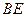 =5,
=5, =8,
=8,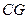 =3,求图中阴影部分面积。
=3,求图中阴影部分面积。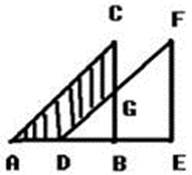
如图,是一块钜形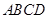 的场地,长
的场地,长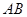 =101米,宽
=101米,宽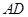 =52米,从
=52米,从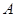 、
、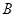 两处入口的中路宽都为1米,两小路汇合处路口宽为2米,其余部分种植草坪面积为___米2
两处入口的中路宽都为1米,两小路汇合处路口宽为2米,其余部分种植草坪面积为___米2
如图
(1)请写出在直角坐标系中的房子的A、B、C、D、E、F、G的坐标。
(2)源源想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图案,并写出平移后的7个点的坐标。
如图 (1) ,将平行四边形ABCD向左平移2个单位长度,可以得到A’B’C’D’,画出平移后的图形,并指出其各个顶点的坐标
小红是某中学的七年级学生,放学后从学校骑自行车回家,学校在她现在位置的北偏东30°方向,距离此处1.5km的地方,她的家在她现在的位置的南偏西45°的方向,距离此处2km,邮局在她现在的位置的北偏西60°的方向,距离此处3km。根据这些信息画一张表示各处位置的简图