如图,矩形ABCD中,AD=3cm,AB=2cm,点E沿A→D方向移动,点F沿D→A方向移动,速度都是1cm/s.如果E、F两点同时分别从A、D出发移动,且当E、F两点相遇即停止.设移动时间是t(s)
(1)四边形BCFE的面积为矩形ABCD面积的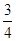 时,t是多少?
时,t是多少?
(2)当BE与CF所在直线的夹角是60°时,t是多少?
(3)四边形BCFE的对角线BF与CE的夹角是90°时,t是多少?
如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,-1),并且与y轴交于点C(0,3),与x轴交于两点A,B.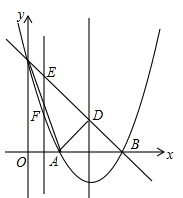
(1)求抛物线的表达式;
(2)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F.问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似?若存在,求出点E的坐标;若不存在,请说明理由.
如图所示,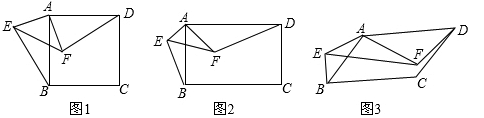
(1)正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF=90°,连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中,BE、DF具有怎样的数量关系和位置关系?结合图(1)给予证明;
(2)将(1)中的正方形ABCD变为矩形ABCD,等腰Rt△AEF变为Rt△AEF,且AD=kAB,AF=kAE,其他条件不变.(1)中的结论是否发生变化?结合图(2)说明理由;
(3)将(2)中的矩形ABCD变为平行四边形ABCD,将Rt△AEF变为△AEF,且∠BAD=∠EAF=a,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用a表示出直线BE、DF形成的锐角β.
学校举办一项小制作评比活动.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的作品件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的件数是12.
请你回答:
(1)本次活动共有件作品参赛;各组作品件数的众数是件;
(2)经评比,第四组和第六组分别有10件和2件作品获奖,那么你认为这两组中哪个组获奖率较高?为什么?
(3)小制作评比结束后,组委会决定从4件最优秀的作品A、B、C、D中选出两件进行全校展示,请用树状图或列表法求出刚好展示作品B、D的概率.
如图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.求证:四边形AECF是平行四边形.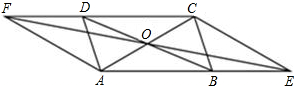
(1)计算:
(2)化简: