阅读下面材料:根据两角和与差的正弦公式,有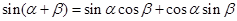 ------①
------① ------②
------②
由①+② 得 ------③
------③
令 有
有
代入③得  .
.
(Ⅰ) 类比上述推理方法,根据两角和与差的余弦公式,证明: ;
;
(Ⅱ)若 的三个内角
的三个内角 满足
满足 ,试判断
,试判断 的形状.
的形状.
(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
已知 ,函数
,函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)已知 ,且
,且 ,求
,求 的值.
的值.
设命题 :实数
:实数 满足
满足 ,其中
,其中 ;命题
;命题 :实数
:实数 满足
满足 ;
;
(1)若 ,且
,且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若 是
是 成立的必要不充分条件,求实数
成立的必要不充分条件,求实数 的取值范围.
的取值范围.
对于函数 ,若存在
,若存在 使得
使得 成立,则称
成立,则称 为
为 的不动点已知函数
的不动点已知函数
(1)若 ,求函数
,求函数 的不动点;
的不动点;
(2)若对任意实数 ,函数
,函数 恒有两个相异的不动点,求
恒有两个相异的不动点,求 的取值范围;
的取值范围;
(3)在(2)的条件下,若 图象上A、B两点的横坐标是函数
图象上A、B两点的横坐标是函数 的不动点,且A、B两点关于直线
的不动点,且A、B两点关于直线 对称,求
对称,求 的最小值
的最小值
已知圆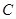 :
: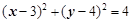 ,直线
,直线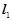 过定点
过定点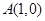

(1)若直线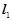 与圆相切,切点为
与圆相切,切点为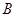 ,求线段
,求线段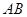 的长度;
的长度;
(2)若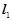 与圆相交于
与圆相交于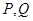 两点,线段
两点,线段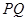 的中点为
的中点为 ,又
,又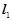 与
与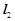 :
: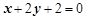 的交点为
的交点为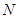 ,判断
,判断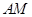 •
•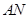 是否为定值,若是,则求出定值;若不是,请说明理由
是否为定值,若是,则求出定值;若不是,请说明理由
如图,四棱锥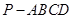 的底面是矩形,侧面
的底面是矩形,侧面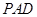 是正三角形,且侧面
是正三角形,且侧面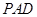
 底面
底面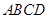 ,
,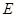 为侧棱
为侧棱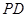 的中点
的中点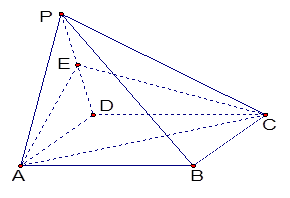
(1)求证: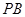 //平面
//平面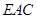 ;
;
(2)求证: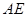 ⊥平面
⊥平面 ;
;
(3)若直线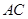 与平面
与平面 所成的角为30
所成的角为30 ,求
,求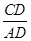 的值
的值