如图所示,质点P在正方形ABCD的四个顶点上按逆时针方向前进.现在投掷一个质地均匀、每个面上标有一个数字的正方体玩具,它的六个面上分别写有两个1、两个2、两个3一共六个数字.质点P从A点出发,规则如下:当正方体上底面出现的数字是1,质点P前进一步(如由A到B);当正方体上底面出现的数字是2,质点P前进两步(如由A到C),当正方体上底面出现的数字是3,质点P前进三步(如由A到D).在质点P转一圈之前连续投掷,若超过一圈,则投掷终止.
(1)求质点P恰好返回到A点的概率;
(2)在质点P转一圈恰能返回到A点的所有结果中,用随机变量ξ表示点P恰能返回到A点的投掷次数,求ξ的数学期望.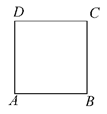
(本题满分14分) 已知F1、F2是椭圆 的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足
的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足 (
( 是坐标原点),
是坐标原点), ,若椭圆的离心率等于
,若椭圆的离心率等于 .
.
(Ⅰ)求直线AB的方程;
(Ⅱ)若三角形ABF2的面积等于4 ,求椭圆的方程;
,求椭圆的方程;
(Ⅲ)在(Ⅱ)的条件下,椭圆上是否存在点M,使得三角形MAB的面积等于8 .
.
(本小题满分12分) 已知函数
(Ⅰ) 当 时,求函数
时,求函数 的最小值,
的最小值,
(Ⅱ)若对任意 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
.(本小题满分12分) 在公差不为零的等差数列 和等比数列
和等比数列 中,已知
中,已知 ,
, ;
;
(Ⅰ) 的公差
的公差 和
和 的公比
的公比 ;
;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和
(本小题满分12分) 四棱锥 的底面与四个侧面的形状和大小如图所示。
的底面与四个侧面的形状和大小如图所示。
(Ⅰ)写出四棱锥 中四对线面垂直关系(不要求证明)
中四对线面垂直关系(不要求证明)
(Ⅱ)在四棱锥 中,若
中,若 为
为 的中点,求证:
的中点,求证: 平面
平面
(Ⅲ)求四棱锥 值。
值。
(本小题满分12分)某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185)得到的频率分布直方图如图所示。
(Ⅰ)求第3、4、5组的频率;
(Ⅱ)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求:第4组至少有一名学生被甲考官面试的概率?