某大学为调查来自南方和北方的同龄大学生的身高差异,从2011级的年龄在18~19岁之间的大学生中随机抽取了来自南方和北方的大学生各10名,测量他们的身高,量出的身高如下:(单位:cm)
南方:158,170,166,169,180,175,171,176,162,163;
北方:183,173,169,163,179,171,157,175,178,166;
(Ⅰ)根据抽测结果,画出茎叶图,并根据你画的茎叶图,对来自南方和北方的大学生的身高作比较,写出两个统计结论;
(Ⅱ)若将样本频率视为总体的概率,现从来自南方的身高不低于170的大学生中随机抽取3名同学,求其中恰有两名同学的身高低于175的概率.
如图,棱柱ABCD—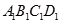 的所有棱长都为2,
的所有棱长都为2,  ,侧棱
,侧棱 与底面ABCD的所成角为60°,
与底面ABCD的所成角为60°, ⊥平面ABCD,
⊥平面ABCD, 为
为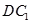 的中点.
的中点.
(1)证明:BD⊥ ;
;
(2)证明: 平面
平面 ;
;
(3)求二面角D

 C的余弦值.
C的余弦值.
某学院为了调查本校学生2011年9月“健康上网”(健康上网是指每天上网不超过两小时)的天数情况,随机抽取了40名本校学生作为样本,统计他们在该月30天内健康上网的天数,并将所得数据分成以下六组:[O,5],(5,1 O], ,(25,30],由此画出样本的频率分布直方图,如图所示.
(1)根据频率分布直方图,求这40名学生中健康上网天数超过20天的人数;
(2)现从这40名学生中任取2名,设Y为取出的2名学生中健康上网天数超过20天的人数,求Y的分布列及其数学期望E(Y).
已知等比数列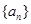 的公比大于1,
的公比大于1,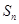 是数列
是数列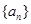 的前n项和,
的前n项和,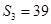 ,且
,且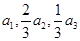 依次成等差数列.
依次成等差数列.
(1)求数列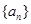 的通项公式;
的通项公式;
(2)若数列 满足:
满足:
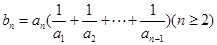 ,求数列
,求数列 的前n项和
的前n项和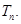
设函数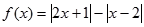 .
.
(1)求不等式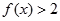 的解集;
的解集;
(2)若 ,
,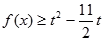 恒成立,求实数他t的取值范围.
恒成立,求实数他t的取值范围.
在直角坐标系xoy中,直线 的参数方程为
的参数方程为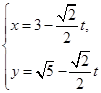 (t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为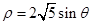 。
。
(1)求圆C的直角坐标方程;
(2)设圆C与直线 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为 ,求|PA|+|PB|.
,求|PA|+|PB|.