如图,棱柱ABCD—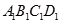 的所有棱长都为2,
的所有棱长都为2,  ,侧棱
,侧棱 与底面ABCD的所成角为60°,
与底面ABCD的所成角为60°, ⊥平面ABCD,
⊥平面ABCD, 为
为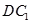 的中点.
的中点.
(1)证明:BD⊥ ;
;
(2)证明: 平面
平面 ;
;
(3)求二面角D

 C的余弦值.
C的余弦值.
(本小题满分12 分)
已知{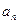 }是整数组成的数列,a1 = 1,且点
}是整数组成的数列,a1 = 1,且点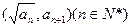 在函数
在函数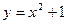 的图象上,
的图象上,
(1)求数列{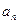 }的通项公式;
}的通项公式;
(2)若数列{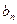 }满足
}满足 = 1,
= 1,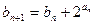 ,求证:
,求证:
(本小题满分12 分)
从甲地到乙地一天共有A、B 两班车,由于雨雪天气的影响,一段时间内A 班车正点到达乙地的概率为0.7,B 班车正点到达乙地的概率为0.75。
(1)有三位游客分别乘坐三天的A 班车,从甲地到乙地,求其中恰有两名游客正点到达的概率(答案用数字表示)。
(2)有两位游客分别乘坐A、B 班车,从甲地到乙地,求其中至少有1 人正点到达的概率(答案用数字表示)。
(本小题满分12 分)
已知函数 的最大值为1.
的最大值为1.
(1)求常数a 的值;
(2)求 的单调递增区间;
的单调递增区间;
(3)求 ≥ 0 成立的x 的取值集合.
≥ 0 成立的x 的取值集合.
(本小题满分14分)如下图(5),在三棱锥 中,
中, 分别是
分别是 的中点,
的中点, ,
, 。
。
(1)求证: 平面
平面 ;
;
(2)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(3)求点 到平面
到平面 的距离。
的距离。
(本小题满分12分)已知三角形 的三个顶点是
的三个顶点是
(1)求 边上的高所在直线的方程;
边上的高所在直线的方程;
(2)求 边上的中线所在直线的方程。
边上的中线所在直线的方程。