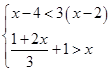如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).
(1)当t为何值时,四边形PQDC是平行四边形.
(2)当t为何值时,以C,D,Q,P为顶点的梯形面积等于60cm2?
(3)是否存在点P,使△PQD是等腰三角形?若存在,请求出所有满足要求的t的值,若不存在,请说明理由.
如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,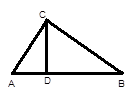
求:(1)△ABC的面积;
(2)CD的长;
(3)作出△ABC的边AC上的中线BE,并求出△ABE的面积;
(4)作出△BCD的边BC边上的高DF,当BD="11cm" 时,试求出DF的长。
如图,建立平面直角坐标系,使B,C的坐标分别为(-2,0)和(2,0).
(1)画出坐标系,写出点A、D的坐标;
(2)若将△ABE向右平移4个单位,然后向上平移3个
单位后,得△A′B′E′,在图中画出△A′B′E′。
开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本;小亮用31元买了同样的钢笔2支和笔记本5本。
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔和笔记本共48件作为奖品,奖给校运会中表现突出的同学,要求笔记本数不少于钢笔数,共有多少种购买方案?请你一一写出。
已知y=x2+px+q,当x=1时,y的值为2;当x=-2时,y的值为2。求x=-3时y的值。
解不等式组,并把解集表示在数轴上