如图甲，在正方形ABCD中，
，点P、Q从A点沿边AB、BC、CD运动，点M从A点沿边AD、DC、CB运动，点P、Q的速度分别为1cm/s，3cm/s ，点M的速度2 cm/s.若它们同时出发，当点M与点Q相遇时，所有点都停止运动.设运动的时间为ts，△PQM的面积为Scm2，则S关于t的函数图象如图乙所示．结合图形，完成以下各题：
（1）当t为何值时，点M与点Q相遇？
（2）填空：
；
；
.
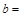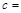（3）当
时,求Ｓ与t的函数关系式;
（4）在整个运动过程中，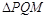
能否为直角三角形？若能，请求出此时t的值；若不能，请说明理由.
李明到某零件加工厂作社会调查，了解到该工厂为了激励工人的工作积极性，实行“月总收入＝基本工资
计件奖金”的方法，并获
得如右表信息．假设生产每件零件奖励
元，每个
工人月基本工资都是
元
求
、的值；若工人小王某月的总收入不低于1800元，
那么小王当月至少要生产零件多少件？
如图，在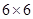
的正方形网格中，每个小正方形的边长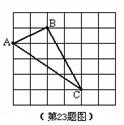
都是1，△ABC的三个顶点都在格点（即小正方形的顶点）上画出线段AC平移后的线段BD，其平移方向为射线AB
的方向，平移的距离为线段AB的长求sin∠DBC的值．
一个不透明的口袋中装有红、黄、绿三种颜色的小球（它们除颜色不同外其余都相同），其中红球2个，黄球1个，从中任意摸出1球是红球的概率是
．求口袋中绿球的个数；
第一次从袋中任意摸出1球（不放回），第二次再任意摸出1球，请你用画树状图或列表的方法表示所有等可能的结果，并求两次都摸到红球的概率．
如图，已知平行四边形ABCD的对角线AC的垂直
平分线与边AD、BC分别交于E、F两点，垂足是点O．
求证：△AOE≌△COF；
问：四边形AFCE是什么特殊的四边形？
（直接写出结论，不需要证明）
在学校组织的“喜迎建党90周年”的知识竞赛中，
每班参加比赛的人数相同，成绩分为A、B、C、D四个
等级，其中相应等级的得分依次记为100分、90分、
80分、70分．学校将某年级的一班和二班的成绩整理
并绘制成如右边的两个统计图：
请你根据图表提供的信息解答下列问题
此次竞赛中二班参加比赛的人数为；
并将下面的表格补充完整
| 众数 |
中位数 |
平均数 |
|
| 一班 |
90 |
||
| 二班 |
100 |
87.6 |
请你从B级以上（包括B级）的人数的角度来比较
一班和二班的成绩