(本题12分)数列{xn}满足x1=1,x2=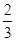 ,且
,且 +
+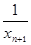 =
= (n≥2),
(n≥2),
(Ⅰ)求数列{xn}的通项公式;
(Ⅱ)令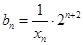 ,求数列{bn}的前n项和
,求数列{bn}的前n项和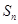 的值.
的值.
(本小题满分12分)在△ABC中,角A,B,C的对边分别为a,b,c,已知c=2,向量m=(c,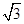 b),
b),
n=(cosC,sinB),且m∥n.
(Ⅰ)求角C的大小;
(Ⅱ)若sin(A+B),sin2A,sin(B-A)成等差数列,求边a的大小.
(本小题满分10分)选修4—5:不等式选讲
已知a+b=1,对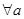 ,b∈(0,+∞),
,b∈(0,+∞), +
+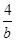 ≥|2x-1|-|x+1|恒成立,
≥|2x-1|-|x+1|恒成立,
(Ⅰ)求 +
+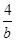 的最小值;
的最小值;
(Ⅱ)求x的取值范围。
(本小题满分10分)选修4—4:坐标系与参数方程
已知直线l经过点P( ,1),倾斜角α=
,1),倾斜角α=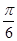 ,圆C的极坐标方程为
,圆C的极坐标方程为 =
= cos(θ-
cos(θ- ).
).
(Ⅰ)写出直线l的参数方程,并把圆C的方程化为直角坐标方程;
(Ⅱ)设l与圆C相交于A,B两点,求点P到A,B两点的距离之积.
(本小题满分10分)选修4—1:几何证明选讲
如图,四边形ACED是圆内接四边形,AD、CE的延长线交于点B,且AD=DE,AB=2AC.
(Ⅰ)求证:BE=2AD;
(Ⅱ)当AC=2,BC=4时,求AD的长.
(本小题满分12分)已知函数f(x)=x+alnx在x=1处的切线l与直线x+2y=0垂直,函数g(x)=f(x)+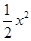 -bx.
-bx.
(Ⅰ)求实数a的值;
(Ⅱ)设x1,x2 (x1<x2)是函数g(x)的两个极值点,若b≥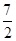 ,求g(x1)-g(x2)的最小值.
,求g(x1)-g(x2)的最小值.