已知数列{ }的前n项和
}的前n项和
(Ⅰ) 求数列{ }的通项公式;(Ⅱ) 设
}的通项公式;(Ⅱ) 设 ,求数列
,求数列 的前
的前 .
.
已知数列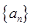 中,
中,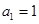 ,
, ,数列
,数列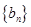 中,
中,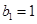 ,且点
,且点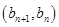 在直线
在直线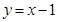 上.
上.
(Ⅰ)求数列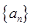 的通项公式;
的通项公式;
(Ⅱ)求数列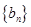 的通项公式;
的通项公式;
(Ⅲ)若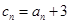 ,求数列
,求数列 的前项和
的前项和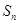 .
.
运货卡车以每小时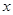 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米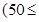
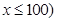 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(1)求这次行车总费用 关于
关于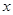 的表达式;
的表达式;
(2)当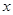 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.
如图,甲船以每小时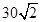 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于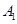 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西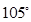 方向的
方向的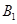 处,此时两船相距
处,此时两船相距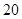 海里,当甲船航行
海里,当甲船航行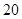 分钟到达
分钟到达 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西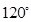 方向的
方向的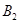 处,此时两船相距
处,此时两船相距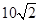 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?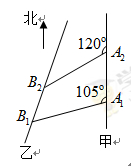
(I)已知集合 若
若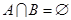 ,求实数
,求实数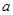 的取值范围;
的取值范围;
(Ⅱ)若不等式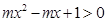 ,对任意实数
,对任意实数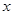 都成立,求
都成立,求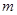 的取值范围.
的取值范围.
在 中,已知
中,已知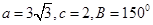 ,求边
,求边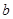 的长及
的长及 的面积.
的面积.