我国是世界上严重缺水的国家之一，城市缺水问题较为突出.某市为了节约生活用水，计划在本市试行居民生活用水定额管理（即确定一个居民月均用水量标准〜用水量不超过a的部分按照平价收费，超过a的部分按照议价收费）.为了较为合理地确定出这个标准，通过抽样获得了 100位居民某年的月均用水量(单位:t)，制作了频率分布直方图，
(I)由于某种原因频率分布直方图部分数据丢失，请在图中将其补充完整；
(II)用样本估计总体，如果希望80%的居民每月的用水量不超出标准&则月均用水量的最低标准定为多少吨，并说明理由；
(III)若将频率视为概率，现从该市某大型生活社区随机调查3位居民的月均用水量(看作有放回的抽样），其中月均用水量不超过（II)中最低标准的人数为x，求x的分布列和均值.
（本小题满分12分）
已知定直线l:x=1和定点M(t,0)(t∈R),动点P到M的距离等于点P到直线l距离的2倍。
（1）求动点P的轨迹方程，并讨论它表示什么曲线；
（2）当t=4时，设点P的轨迹为曲线C，过点M作倾斜角为θ(θ>0)的直线交曲线C于A、B两点，直线l与x轴交于点N。若点N恰好落在以线段AB为直径的圆上，求θ的值。
已知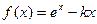
①若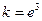
求 
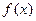的单调区间
②若对任意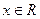
,有
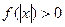恒成立，求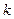
的取值范围？
③ 若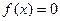
有两相异实根，求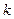的取值范围？
本题满分12分）
2008年中国北京奥运会吉祥物由5个“中国福娃”组成，分别叫贝贝、晶晶、欢欢、迎迎、妮妮（含义：“北京欢迎你”）。现有8个相同的盒子，每个盒子中有一只福娃，每种福娃的数量如下表：
| 福娃名称 |
贝贝 |
晶晶 |
欢欢 |
迎迎 |
妮妮 |
| 数量 |
2 |
2 |
2 |
1 |
1 |
从中随机地选取5只。
（1）求选取的5只恰好组成完整“奥运会吉祥物”的概率；
（2）若完整地选取奥运会吉祥物记100分；若选出的5只中仅差一种记80分；差两种记60分；……。设ξ表示所得的分数，求ξ的分布列和期望值。（结果保留一位小数）
在三棱柱ABC-A1B1C1中，∠ACB=
，AC=CB=1，D1是线段A1B1上一动点（可以与A1或B1重合）。过D1和CC1的平面与AB交于D。
(1）若四边形CDD1C1总是矩形，求证：三棱柱ABC-A1B1C1为直三棱柱；
(2)在（1）的条件下，求二面角B-AD1-C的取值范围。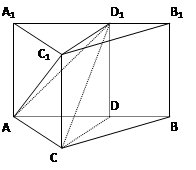
已知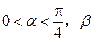
为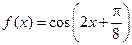
的最小正周期，向量
，且a•b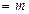
(m为实常数) ．求
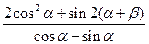的值．