已知函数 (a ,b
(a ,b R,e为自然对数的底数),
R,e为自然对数的底数), .
.
(I )当b=2时,若 存在单调递增区间,求a的取值范围;
存在单调递增区间,求a的取值范围;
(II)当a>0 时,设 的图象C1与
的图象C1与 的图象C2相交于两个不同的点P、Q,过线段PQ的中点作x轴的垂线交C1于点
的图象C2相交于两个不同的点P、Q,过线段PQ的中点作x轴的垂线交C1于点 ,求证
,求证 .
.
已知函数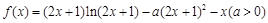 .
.
(1)若函数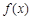 在
在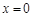 处取极值,求
处取极值,求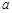 的值;
的值;
(2)如图,设直线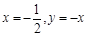 将坐标平面分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个区域(不含边界),若函数
将坐标平面分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个区域(不含边界),若函数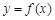 的图象恰好位于其中一个区域内,判断其所在的区域并求对应的
的图象恰好位于其中一个区域内,判断其所在的区域并求对应的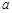 的取值范围;
的取值范围;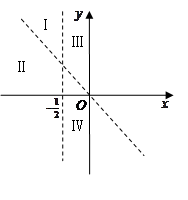
(3)比较 与
与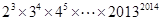 的大小,并说明理由.
的大小,并说明理由.
如图所示,在棱长为2的正方体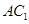 中,点
中,点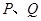 分别在棱
分别在棱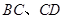 上,满足
上,满足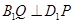 ,且
,且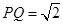 .
.
(1)试确定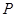 、
、 两点的位置.
两点的位置.
(2)求二面角 大小的余弦值.
大小的余弦值.
已知曲线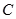 的极坐标方程为
的极坐标方程为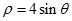 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴的非负半轴建立平面直角坐标系,并与极坐标系取相同的单位长度,直线l的参数方程为
轴的非负半轴建立平面直角坐标系,并与极坐标系取相同的单位长度,直线l的参数方程为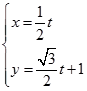 (
(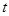 为参数),求直线l被曲线
为参数),求直线l被曲线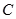 截得的线段长度.
截得的线段长度.
已知矩阵M = ,N =
,N =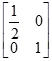 ,试求曲线
,试求曲线 在矩阵MN变换下的函数解析式.
在矩阵MN变换下的函数解析式.
在数列 中,
中,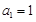 ,且对任意的
,且对任意的 ,
,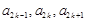 成等比数列,其公比为
成等比数列,其公比为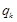 .
.
(1)若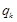 =2(
=2( ),求
),求 ;
;
(2)若对任意的 ,
,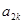 ,
,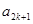 ,
,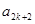 成等差数列,其公差为
成等差数列,其公差为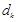 ,设
,设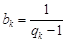 .
.
①求证: 成等差数列,并指出其公差;
成等差数列,并指出其公差;
②若 =2,试求数列
=2,试求数列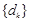 的前
的前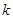 项的和
项的和 .
.