如图, 是南北方向的一条公路,
是南北方向的一条公路, 是北偏东
是北偏东 方向的一条公路,某风景区的一段边界为曲线
方向的一条公路,某风景区的一段边界为曲线 .为方便游客光,拟过曲线
.为方便游客光,拟过曲线 上的某点分别修建与公路
上的某点分别修建与公路 ,
, 垂直的两条道路
垂直的两条道路 ,且
,且 的造价分别为
的造价分别为 万元/百米,
万元/百米, 万元/百米,建立如图所示的直角坐标系
万元/百米,建立如图所示的直角坐标系 ,则曲线符合函数
,则曲线符合函数 模型,设
模型,设 ,修建两条道路
,修建两条道路 的总造价为
的总造价为 万元,题中所涉及的长度单位均为百米.
万元,题中所涉及的长度单位均为百米.
(1)求 解析式;
解析式;
(2)当 为多少时,总造价
为多少时,总造价 最低?并求出最低造价.
最低?并求出最低造价.
有一个正四棱台形状的油槽,可以装油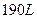 ,假如它的两底面边长分别等于
,假如它的两底面边长分别等于 和
和 ,求它的深度为多少
,求它的深度为多少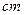 ?(1L=1000cm3)
?(1L=1000cm3)
、已知圆O:x2+y2=13
(1)证明:点A(-1,5)在圆O外。
(2)如图所示,经 过圆O上任P一点作y轴的垂线,垂足为Q,求线段PQ的中点M的轨迹方程。
过圆O上任P一点作y轴的垂线,垂足为Q,求线段PQ的中点M的轨迹方程。
平面直角坐标系中有A(0,1),B(2,1),C(3,4),D(2,4)
(1)求△ABC外接圆M的方程;
(2)若直线 被圆M所截得的弦的
被圆M所截得的弦的 中点恰为点D,求直线
中点恰为点D,求直线 的方程。
的方程。
、已知点P(-1,1),点Q(2,2),直线 :x+my+m=0
:x+my+m=0
(1)无论m取何值,直线 恒过一定点,求该定点的坐标;
恒过一定点,求该定点的坐标;
(2)若直线 与线段PQ有交点,求m的范围。
与线段PQ有交点,求m的范围。
 一条光线从点P(6,4)射出,经y轴反射后经过点Q(3,10),求入射光线和反射光线所在直线方程。 (12分)
一条光线从点P(6,4)射出,经y轴反射后经过点Q(3,10),求入射光线和反射光线所在直线方程。 (12分)