已知数列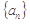 满足
满足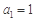 ,且
,且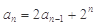 (n
(n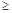 2且n∈N*).
2且n∈N*).
(Ⅰ)求数列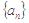 的通项公式;
的通项公式;
(Ⅱ)设数列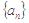 的前n项之和
的前n项之和 ,求
,求 ,并证明:
,并证明: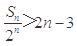 .
.
在等差数列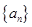 和等比数列
和等比数列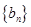 中,a1=2, 2b1=2, b6=32,
中,a1=2, 2b1=2, b6=32,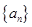 的前20项和S20=230.
的前20项和S20=230.
(Ⅰ)求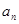 和
和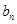 ;
;
(Ⅱ)现分别从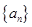 和
和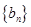 的前4中各随机抽取一项,写出相应的基本事件,并求所取两项中,满足an>bn的概率.
的前4中各随机抽取一项,写出相应的基本事件,并求所取两项中,满足an>bn的概率.
已知函数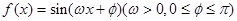 为偶函数,周期为2
为偶函数,周期为2 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若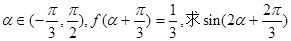 的值.
的值.
设函数f(x)=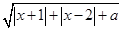 .
.
(Ⅰ)当a=-5时,求函数f(x)的定义域;
(II)若函数f(x)的定义域为R,试求a的取值范围.
已知曲线 的参数方程为
的参数方程为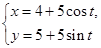 (
(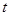 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,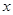 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为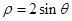 .
.
(Ⅰ)把 的参数方程化为极坐标方程;
的参数方程化为极坐标方程;
(Ⅱ)求 与
与 交点的极坐标(
交点的极坐标(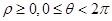 ).
).
如图, 为△
为△ 外接圆的切线,
外接圆的切线,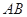 的延长线交直线
的延长线交直线 于点
于点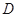 ,
, 分别为弦
分别为弦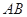 与弦
与弦 上的点,且
上的点,且 ,
,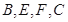 四点共圆.
四点共圆. 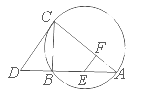
(Ⅰ)证明: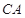 是△
是△ 外接圆的直径;
外接圆的直径;
(Ⅱ)若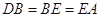 ,求过
,求过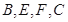 四点的圆的面积与△
四点的圆的面积与△ 外接圆面积的比值.
外接圆面积的比值.