如图,在平面直角坐标系中,△AOB是直角三角形,∠AOB=90°,边AB与y轴交于点C.
(1)若∠A=∠AOC,试说明:∠B=∠BOC;
(2)延长AB交x轴于点E,过O作OD⊥AB,若∠DOB=∠EOB,∠A=∠E,求∠A的度数;
(3)如图,OF平分∠AOM,∠BCO的平分线交FO的延长线于点P,∠A=40°,当△ABO绕O点旋转时(边AB与y轴正半轴始终相交于点C),问∠P的度数是否发生改变?若不变,求其度数;若改变,请说明理由.
在 中, , 是 内一点,连接 , ,在 左侧作 ,使 ,以 和 为邻边作 ,连接 , .
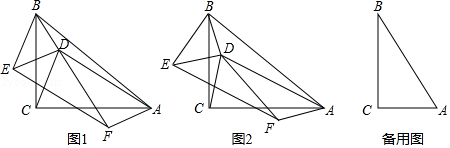
(1)若 , .
①如图1,当 , , 三点共线时, 与 之间的数量关系为 .
②如图2,当 , , 三点不共线时,①中的结论是否仍然成立?请说明理由.
(2)若 , , ,且 , , 三点共线,求 的值.
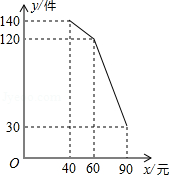
某商场销售一种商品的进价为每件30元,销售过程中发现月销售量 (件 与销售单价 (元 之间的关系如图所示.
(1)根据图象直接写出 与 之间的函数关系式.
(2)设这种商品月利润为 (元 ,求 与 之间的函数关系式.
(3)这种商品的销售单价定为多少元时,月利润最大?最大月利润是多少?
如图,在 中, , 是 上一点,过 , , 三点的 交 于点 ,连接 , ,点 是线段 上的一点,连接 ,其中 .
(1)求证: 是 的切线.
(2)若 是 的中点, , ,求 的长.

如图为某海域示意图,其中灯塔 的正东方向有一岛屿 .一艘快艇以每小时 的速度向正东方向航行,到达 处时测得灯塔 在东北方向上,继续航行 ,到达 处时测得灯塔 在北偏东 方向上,同时测得岛屿 恰好在 处的东北方向上,此时快艇与岛屿 的距离是多少?(结果精确到 .参考数据: , ,

如图,在平面直角坐标系中,一次函数 的图象与 轴交于点 ,与反比例函数 的图象交于 , 两点,点 在第一象限,纵坐标为4,点 在第三象限, 轴,垂足为点 , .
(1)求反比例函数和一次函数的解析式.
(2)连接 , ,求四边形 的面积.
