阅读下面材料:
根据两角和与差的正弦公式,有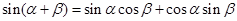 ------①
------①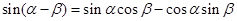 ------②
------②
由①+② 得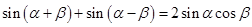 ------③
------③
令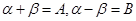 有
有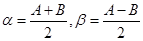
代入③得 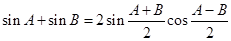 .
.
(1) 类比上述推理方法,根据两角和与差的余弦公式,证明: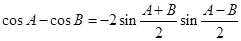 ;
;
(2)若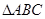 的三个内角
的三个内角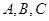 满足
满足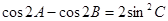 ,直接利用阅读材料及(1)中的结论试判断
,直接利用阅读材料及(1)中的结论试判断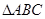 的形状.
的形状.
(本小题满分5分)选修4—5:不等式选讲
已知函数
(1)作出函数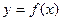 的图象;
的图象;
(2)解不等式
(本小题满分5分)选修4—4:坐标系与参数方程
已知直线 与圆
与圆 (
( 为参数),试判断它们的公共点个数。
为参数),试判断它们的公共点个数。
(本小题满分5分)选修4 —2:矩阵与变换
—2:矩阵与变换
二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成(-1,1)与(1,-2)。若直线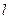 在变换M作用下得到了直线
在变换M作用下得到了直线 求直线
求直线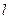 的方程。
的方程。
(本小题满分14分)
在平面直角坐标系中, 为坐标原点,已知两点
为坐标原点,已知两点 ,若动点
,若动点 满足
满足 且点
且点 的轨迹与抛物线
的轨迹与抛物线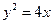 交于
交于 两点.
两点.
(1)求证: ;
;
(2)在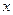 轴上是否存在一点
轴上是否存在一点 ,使得过点
,使得过点 的直线
的直线 交抛物线
交抛物线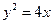 于
于 两点,并以线段
两点,并以线段 为直径的圆都过原点。若存在,请求出
为直径的圆都过原点。若存在,请求出 的值及圆心
的值及圆心 的轨迹方
的轨迹方 程;若不存在,请说明理由.
程;若不存在,请说明理由.
(本小题满分14分)已知函数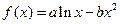 图象上一点
图象上一点 处的切线方程为
处的切线方程为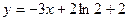 .
.
(1)求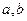 的值;
的值;
(2)若方程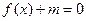 在
在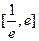 内有两个不等实根,求
内有两个不等实根,求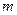 的取值范围(其中
的取值范围(其中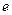 为自然对数的底数);
为自然对数的底数);