已知:在四边形ABCD中,AC = BD,AC与BD交于点O,∠DOC = 60°.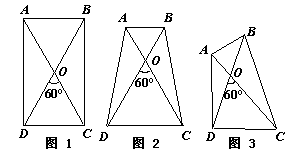
(1)当四边形ABCD是平行四边形时(如图1),证明AB + CD = AC;
(2)当四边形ABCD是梯形时(如图2),AB∥CD,线段AB、CD和线段AC之间的数量关系是_____________________________;
(3)如图3,四边形ABCD中,AB与CD不平行,结论AB + CD = AC是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
如图,已知二次函数的图象经过点A(3,3)、B(4,0)和原点O.P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.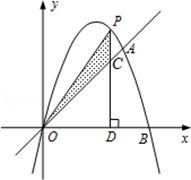
(1)求出二次函数的解析式;
(2)当点P在直线OA的上方时,用含m的代数式表示线段PC的长,并求线段PC的最大值;
(3)当m>0时,探索是否存在点P,使得△PCO为等腰三角形,如果存在,请直接写出所有P的坐标;如果不存在,请说明理由.
如图①,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.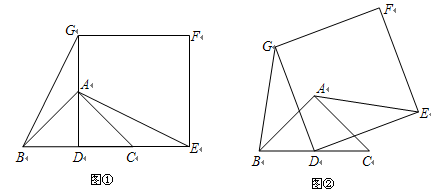
(1)试猜想线段BG和AE的数量关系,请直接写出你得到的结论.
(2)将正方形DEFG绕点D逆时针方向旋转一定角度后(旋转角度大于0°,小于或等于360°),如图②,通过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由.
(3)若BC=DE=2,在(2)的旋转过程中,当AE为最大值时,求AF的值.
小明和小亮进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡底跑到坡顶再原路返回坡底.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小明在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).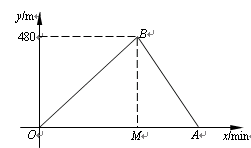
(1)求小明上、下坡的速度及A点的坐标;
(2)小亮上坡平均速度是小明上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
如图1,抛物线 与x轴交于A、C两点,与y轴交于B点,与直线y=kx+b交于A、D两点.
与x轴交于A、C两点,与y轴交于B点,与直线y=kx+b交于A、D两点.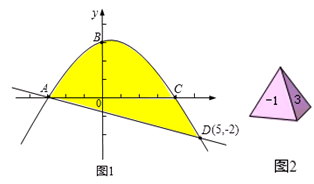
(1)求A、C两点坐标和直线AD的解析式;
(2)如图2,质地均匀的正四面体骰子的各个面上依次标有数字-1、1、3、4.随机抛掷这枚骰子两次,把第一次着地一面的数字m记做P点的横坐标,第二次着地一面的数字n记做P点的纵坐标.则点P(m,n)落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
如图,以线段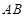 为直径的⊙
为直径的⊙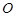 交线段
交线段 于点
于点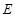 ,点
,点 是弧AE的中点,
是弧AE的中点,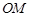 交
交 于点
于点 ,
, °,
°, ,
, .
.
(1) =°;
=°;
(2)求证:BC是⊙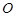 的切线;
的切线;
(3)求MD的长度.