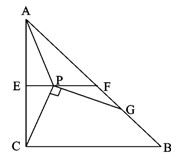
如图，Rt△ABC中，∠C= Rt∠，AC=BC=2，E，F分别为AC，AB的中点，连结EF。
现将一把直角尺放在给出的图形上，使直角顶点P在线段EF（包括端点）上滑动，直角的
一边始终经过点C，另一边与BF相交于G，连结AP。
（1）求证：PC=PA=PG；
（2）设EP=
，四边形BCPG的面积为
，求与之间的函数解析式，现有三个数
，
， 
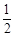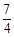试通过计算说明哪几个数符合值的要求，并求出符合值时的的值。
（3）当直角顶点P滑动到点F时，再将直角尺绕点F顺时针旋转，两直角边分别交AC，BC于点M，N，连结MN。当旋转到使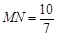
时，求△APM的周长。
先化简，再求值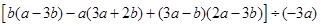
，其中 
、
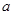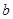满足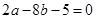
．
解方程（每题5分，共10分）
（1）
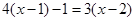
（2）
计算
（1）如图1，已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E． 证明：DE=BD+CE．
如图2，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．
（3）拓展与应用：如图3，D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状． 
若x²y+xy²=30，xy=6，求下列代数式的值：（1）x²+y²；（2）x-y.