计算
某市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
| 组别 |
成绩x |
频数(人数) |
| 第1组 |
25≤x<30 |
4 |
| 第2组 |
30≤x<35 |
8 |
| 第3组 |
35≤x<40 |
16 |
| 第4组 |
40≤x<45 |
a |
| 第5组 |
45≤x<50 |
10 |
请结合图表完成下列各题:
(1)表中a的值为____________;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?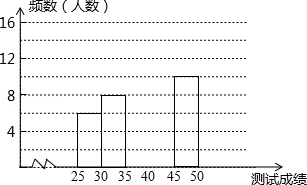
某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克。求该种干果的第一次进价是每千克多少元?
如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(﹣2,2),B(0,5),C(0,2).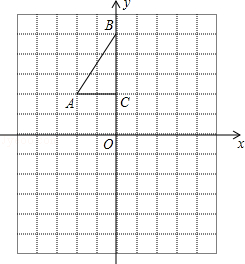
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(﹣2,﹣6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标____________________.
解方程:
(1)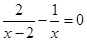
(2)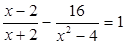
如图所示,在直角梯形ABCD中,AD//BC,∠A=90°,AB=12,BC=21,AD=16。动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动。设运动的时间为t(秒)。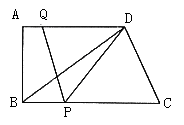
(1)设△DPQ的面积为S,用含有t的代数式表示S。
(2)当t为何值时,四边形PCDQ是平行四边形?