P、Q、R、S四个小球分别从正方形ABCD的四个定点A、B、C、D点出发,以同样的速度分别沿AB、BC、CD、DA的方向滚动,其终点分别是B、C、D、A。不管滚动多长时间,求证:四边形PQRS为正方形;
连结对角线AC、BD、PR、SQ,你发现四条对角线有何关系?
根据此图,若有四个全等的直角三角形,你能否拼成一个正方形?若这个三角形直角边为a、b,斜边问c,你能否根据面积推导出勾股定理?
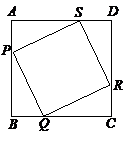
在数轴上表示–2和10两点之间插入三个点,使这5个点每相邻两点之间的距离相等,求这三个点所表示的数。
如图,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形.

(1)拼成的正方形的面积与边长分别是多少?
(2)如图所示,以数轴的单位长度的线段为边作一个直角三角形,以数轴的-1点为圆心,直角三角形的最大边为半径画弧,交数轴正半轴于点A,那么点A表示的数是多少?点A表示的数的相反数是多少?
(3)你能把十个小正方形组成的图形纸,剪开并拼成正方形吗?若能,请画出示意图,并求它的边长
如图,半径为1个单位的圆片上有一点Q与数轴上的原点重合(提示:圆的周长C=2 r,
r,  保留)
保留)
(1)把圆片沿数轴滚动1周,点Q到达数轴上点A的位置,点A表示的数是___;
(2)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依
次运动情况记录如下:+2, -1, -5, +4, +3, -2
①第几次滚动后,Q点距离原点最近?第几次滚动后,Q点距离原点最远?
②当圆片结束运动时,Q点运动的路程共有多少?此时点Q所表示的数是多少?
已知已知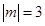 ,
,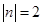 ,且
,且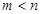 ,求
,求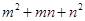 的值
的值
(1)求出下列各数:①2的平方根;②-27的立方根;③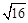 的算术平方根.
的算术平方根.
(2)将(1)中求出的每个数准确地表示在数轴上.
(3)将(1)中求出的每个数按从小到大的顺序排列,并用“﹤”连接.