到高中时,我们将学习虚数i,(i叫虚数单位).规定i2=-1,如-2=2×(-1)=(± )2·i2=(±
)2·i2=(± i)2,那么x2=-2的根就是:x1=
i)2,那么x2=-2的根就是:x1= i,x2=-
i,x2=- i.试求方程x2+2x+3=0的根.
i.试求方程x2+2x+3=0的根.
(年湖南湘西22分)如图,抛物线y=ax2+bx+c关于y轴对称,它的顶点在坐标原点O,点B(2,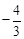 )和点C(﹣3,﹣3)两点均在抛物线上,点F(0,
)和点C(﹣3,﹣3)两点均在抛物线上,点F(0, )在y轴上,过点(0,
)在y轴上,过点(0, )作直线l与x轴平行.
)作直线l与x轴平行.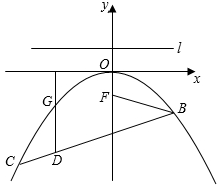
(1)求抛物线的解析式和直线BC的解析式.
(2)设点D(x,y)是线段BC上的一个动点(点D不与B,C重合),过点D作x轴的垂线,与抛物线交于点G.设线段GD的长度为h,求h与x之间的函数关系式,并求出当x为何值时,线段GD的长度h最大,最大长度h的值是多少?
(3)若点P(m,n)是抛物线上位于第三象限的一个动点,连接PF并延长,交抛物线于另一点Q,过点Q作QS⊥l,垂足为点S,过点P作PN⊥l,垂足为点N,试判断△FNS的形状,并说明理由;
(4)若点A(﹣2,t)在线段BC上,点M为抛物线上的一个动点,连接AF,当点M在何位置时,MF+MA的值最小,请直接写出此时点M的坐标与MF+MA的最小值.
(年湖南衡阳10分)二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点为A(﹣3,0)、B(1,0)两点,与y轴交于点C(0,﹣3m)(其中m>0),顶点为D.
(1)求该二次函数的解析式(系数用含m的代数式表示);
(2)如图①,当m=2时,点P为第三象限内的抛物线上的一个动点,设△APC的面积为S,试求出S与点P的横坐标x之间的函数关系式及S的最大值;
(3)如图②,当m取何值时,以A、D、C为顶点的三角形与△BOC相似?
(2014年湖北孝感12分)如图1,矩形ABCD的边AD在y轴上,抛物线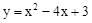 经过点A、点B,与x轴交于点E、点F,且其顶点M在CD上.
经过点A、点B,与x轴交于点E、点F,且其顶点M在CD上.
(1)请直接写出下列各点的坐标:A ,B ,C ,D ;
(2)若点P是抛物线上一动点(点P不与点A、点B重合),过点P作y轴的平行线l与直线AB交于点G,与直线BD交于点H,如图2.
①当线段PH=2GH时,求点P的坐标;
②当点P在直线BD下方时,点K在直线BD上,且满足△KPH∽△AEF,求△KPH面积的最大值.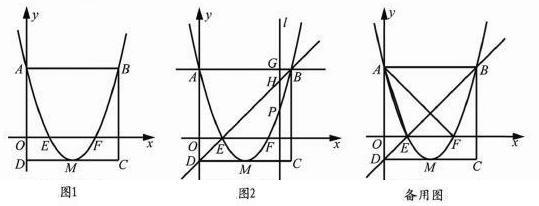
(年贵州黔西南16分)如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.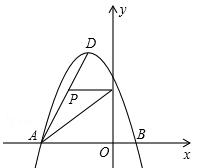
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
(年贵州黔南12分)如图,在平面直角坐标系中,顶点为(4,﹣1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3).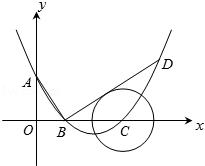
(1)求此抛物线的解析式
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明;
(3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积.