计算: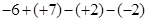
如图,抛物线y=ax2+bx-4与x轴交于A(4,0)、B(-2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.女女求该抛物线的解析式;
当动点P运动到何处时,BP2=BD•BC;
当△PCD的面积最大时,求点P的坐标.
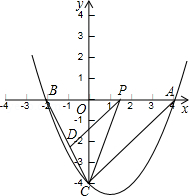
有四张形状、大小和质地相同的卡片A、B、C、D,正面分别写有一个正多边形(所有正多边形的边长相等),把四张卡片洗匀后正面朝下放在桌面上,从中随机抽取一张(不放回),接着再随机抽取一张.
请你用画树形图或列表的方法列举出可能出现的所有结果;
如果在(1)中各种结果被选中的可能性相同,求两次抽取的正多边形能构成平面镶嵌的概率;
若两种正多边形构成平面镶嵌,p、q表示这两种正多边形的个数,x、y表示对应正多边形的每个内角的度数,则有方程px+qy=360,求每种平面镶嵌中p、q的值.
如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.请写出旋转中心的坐标是,旋转角是度;
以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形;
设Rt△ABC两直角边BC=a、AC=b、斜边AB=c,利用变换前后所形成的图案证明勾股定理.

如图,AB是⊙O的直径,AC是弦,OD⊥AC于点D,过点A作⊙O的切线AP,AP与OD的延长线交于点P,连接PC、BC.猜想:线段OD与BC有何数量和位置关系,并证明你的结论.
求证:PC是⊙O的切线
