已知抛物线y＝ax2＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．
(1)求抛物线的函数关系式；
(2)设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；
(3)在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．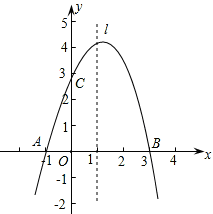
（本题10分）已知：如图，在△ABC中，AB＝AC，点D是边BC的中点，以BD为直径作圆O，交边AB于点P，连接PC，交AD于点E．
（1）求证：AD是圆O的切线：
（2）若PC是圆O的切线，BC＝8，求DE的长．
（本题10分）如图，在⊙O中，直径AB=2，CA切⊙O于A，BC交⊙O于D，若∠C=45°，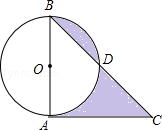
（1）求BD的长；
（2）求阴影部分的面积.
（本题10分）如图，正方形网格中每个小正方形边长都是1，每个小格的顶点叫格点，以格点为顶点的三角形叫做格点三角形．
（1）格点△ABC的面积为；
（2）画出格点△ABC绕点C逆时针旋转90°后的△A1B1C1，并求出在旋转过程中，点B所经过的路径长．
（本题10分）如图，已知AD是△ABC的高，AE是△ABC的外接圆的直径．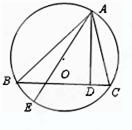
（1）求证AC·AB＝AD·AE；
（2）若AB＝8，AC＝5，AD＝4，求⊙O的面积．
（本题共10分） 已知关于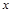
的方程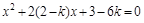
，
（1）若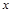=1是此方程的一根，求
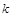的值及方程的另一根；
（2）试说明无论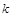取什么实数值，此方程总有实数根．