一台机器使用的时间较长，但还可以使用，它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器的运转的速度而变化，下表为抽样试验的结果：
| 转速x(转/秒) |
2 |
4 |
5 |
6 |
8 |
| 每小时生产有缺点的零件数y（件） |
30 |
40 |
60 |
50 |
70 |
（1）画散点图
（2）如果y对x有线性相关关系，求回归直线方程；
（3）若实际生产中，允许每小时的产品中有缺点的零件最多为89个，那么机器的运转速度应控制在什么范围内？(参考数值：
，
)
已知函数
，
（1）求函数
的最小正周期；
（2）若
，求
的值．
已知焦点在x轴上的双曲线C的两条渐近线过坐标原点，且两条渐近线与以点A (0，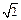
)为圆心，1为半径的圆相切，又知C的一个焦点与A关于y = x对称．
（1）求双曲线C的方程；
（2）若Q是双曲线线C上的任一点，F1，F2为双曲线C的左、右两个焦点，从F1引∠F1QF2的平分线的垂线，垂足为N，试求点N的轨迹方程；
（3）设直线y =" mx" + 1与双曲线C的左支交于A、B两点，另一直线l经过M (–2，0)及AB的中点，求直线l在y轴上的截距b的取值范围．
已知函数
，
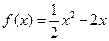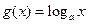。如果函数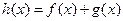
没有极值点，且
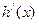存在零点。（1）求
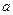的值；（2）判断方程
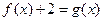根的个数并说明理由；（3）设点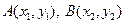
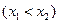是函数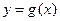
图象上的两点，平行于AB 的切线以
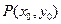为切点，求证：
。
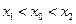已知等差数列
的首项为a，公差为b；等比数列
的首项为b，公比为a，其中a，
，且
．
（1）求a的值；
（2）若对于任意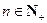
，总存在
，使
，求b的值；
（3）在（2）中，记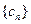
是所有中满足， 的项从小到大依次组成的数列，又记
为的前n项和，
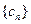的前n项和，求证：≥
如图，摩天轮的半径为40m，摩天轮的圆心O距地面的高度为50m，摩天轮做匀速转动，每3min转一圈，摩天轮上的点P的起始位置在最低点处．
（1）已知在时刻t (min)时点P距离地面的高度为f (t) = A sin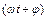 
+ h，求2006min时点距离地面的高度．
（2）求证：不论t为何值，f (t) + f (t + 1) + f (t + 2)是定值．