实践应用（本小题满分6分）有两个可以自由转动的均匀转盘A，B-优题课

实践应用（本小题满分6分）
有两个可以自由转动的均匀转盘A，B都被分成了3等分，并在每一份内均标有数字，如图所示，规则如下：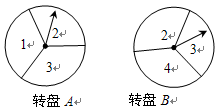

①分别转动转盘A，B；②两个转盘停止后观察两个指针所指份内的数字（若指针停在等分线上，那么重转一次，直到指针指向某一份内为止）．
（1）请用树状图或列表法列出所有可能的结果；
（2）王磊和张浩想用这两个转盘做游戏，他们规定：若“两个指针所指的数字都是方程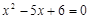的解”时，王磊得1分；若“两个指针所指的数字都不是方程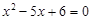的解”时，张浩得3分，这个游戏公平吗？为什么？

科目数学题型解答题难度中等

知识点：利用频率估计概率

先化简，再求值： $(2 x + 1) (2 x - 1) - {(2 x - 3)}^{2}$ ，其中 $x = - 1$ ．

如图，在平面直角坐标系 $xOy$ 中，抛物线 $y = - \frac{1}{4} x^{2} + \frac{3}{2} x + 4$ 与两坐标轴分别相交于 $A$ ， $B$ ， $C$ 三点．

（1）求证： $∠ ACB = 90 °$ ；

（2）点 $D$ 是第一象限内该抛物线上的动点，过点 $D$ 作 $x$ 轴的垂线交 $BC$ 于点 $E$ ，交 $x$ 轴于点 $F$ ．

①求 $DE + BF$ 的最大值；

②点 $G$ 是 $AC$ 的中点，若以点 $C$ ， $D$ ， $E$ 为顶点的三角形与 $ΔAOG$ 相似，求点 $D$ 的坐标．

如图， $ΔABC$ 是 $⊙ O$ 的内接三角形，过点 $C$ 作 $⊙ O$ 的切线交 $BA$ 的延长线于点 $F$ ， $AE$ 是 $⊙ O$ 的直径，连接 $EC$ ．

（1）求证： $∠ ACF = ∠ B$ ；

（2）若 $AB = BC$ ， $AD ⊥ BC$ 于点 $D$ ， $FC = 4$ ， $FA = 2$ ，求 $AD \cdot AE$ 的值．

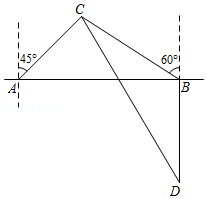
如图， $A$ ， $B$ 是海面上位于东西方向的两个观测点，有一艘海轮在 $C$ 点处遇险发出求救信号，此时测得 $C$ 点位于观测点 $A$ 的北偏东 $45 °$ 方向上，同时位于观测点 $B$ 的北偏西 $60 °$ 方向上，且测得 $C$ 点与观测点 $A$ 的距离为 $25 \sqrt{2}$ 海里．

（1）求观测点 $B$ 与 $C$ 点之间的距离；

（2）有一艘救援船位于观测点 $B$ 的正南方向且与观测点 $B$ 相距30海里的 $D$ 点处，在接到海轮的求救信号后立即前往营救，其航行速度为42海里 $/$ 小时，求救援船到达 $C$ 点需要的最少时间．

一次函数 $y = kx + b (k \neq 0)$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象相交于 $A (2, 3)$ ， $B (6, n)$ 两点．

（1）求一次函数的解析式；

（2）将直线 $AB$ 沿 $y$ 轴向下平移8个单位后得到直线 $l$ ， $l$ 与两坐标轴分别相交于 $M$ ， $N$ ，与反比例函数的图象相交于点 $P$ ， $Q$ ，求 $\frac{PQ}{MN}$ 的值．

试卷网试题网古诗词网作文网范文网