活动探究（本小题满分7分）
如图，已知二次函数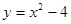
，将
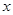轴下方的图象沿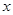轴翻折，得到一个新图象（图中的实线）.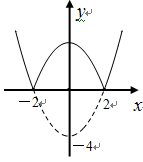
根据新图像回答问题：
（1）当x= ▲ 时，函数y有最小值.
（2）当y随x的增大而增大时，自变量x的范围是 ▲ .
（3）当a＜4时，探究一次函数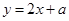
的图像与新图象公共点的个数情况.
如图，在直角坐标系xOy中，直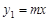线
与双曲线
相交于
A（－1，a）、B两点，BC⊥x轴，垂足为C，△BOC的面积是1．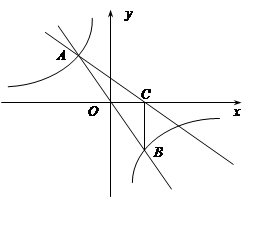
（1）求m、n的值；
（2）求直线AC的解析式；
（3）结合图象直接写出当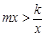
时，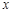
的取值范围．
如图，△ABC为等腰三角形，AB＝AC，O是底边BC的中点，⊙O与腰AB相切于点D，求证：AC与⊙O相切。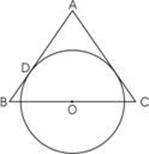
（本题满分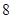
分）商店只有雪碧、可乐、果汁、奶汁四种饮料，每种饮料数量充足，某同学去该店购买饮料，每种饮料被选中的可能性相同．
（1）若他去买一瓶饮料，则他买到奶汁的概率是;
（2）若他两次去买饮料，每次买一瓶，且两次所买饮料品种不同，请用树状图或列表法求出他恰好买到雪碧和奶油的概率．
（本题满分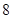
分）如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．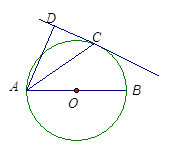
（1）求证：AD⊥DC；
（2）若AD＝2，AC＝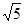
，求AB的长．
已知⊙O的半径为13cm，弦AB∥CD，AB＝24cm，CD＝10cm，求AB和CD之间的距离．