(本小题满分12分)某单位为了提高员工素质,举办了一场跳绳比赛,其中男员工12人,女员工18人,其成绩编成如图所示的茎叶图(单位:分),分数在175分以上(含175分)者定为“运动健将”,并给予特别奖励,其他人员则给予“运动积极分子”称号.
⑴ 若用分层抽样的方法从“运动健将”和“运动积极分子”中抽取10人,然后再从这10人中选4人,求至少有1人是“运动健将”的概率;
⑵ 若从所有“运动健将”中选3名代表,用 表示所选代表中女“运动健将”的人数,试写出
表示所选代表中女“运动健将”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望.
((本小题满分14分)
设数列 为等比数列,数列
为等比数列,数列 满足
满足 ,
, ,已知
,已知 ,
, ,其中
,其中 .
.
(Ⅰ)求数列 的首项和公比;
的首项和公比;
(Ⅱ)当 时,求
时,求 ;
;
(Ⅲ)设 为数列
为数列 的前
的前 项和,若对于任意的正整数
项和,若对于任意的正整数 ,都有
,都有 ,求实数
,求实数 的取值范围.
的取值范围.
((本小题满分14分)
给定椭圆 :
:
 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 的“伴随圆”. 已知椭圆
的“伴随圆”. 已知椭圆 的两个焦点分别是
的两个焦点分别是 ,椭圆
,椭圆 上一动点
上一动点 满足
满足 .
.
(Ⅰ)求椭圆 及其“伴随圆”的方程
及其“伴随圆”的方程
(Ⅱ)试探究y轴上是否存在点 (0,
(0,  )
) ,使得过点
,使得过点 作直线
作直线 与椭圆
与椭圆 只有一个交点,且
只有一个交点,且 截椭圆
截椭圆 的“伴随圆”所得的弦长为
的“伴随圆”所得的弦长为 .若存在,请求出
.若存在,请求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(本小题满分12分)
| 日销售量 |
1 |
1.5 |
2 |
| 频数 |
10 |
25 |
15 |
| 频率 |
0.2 |
某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下:
(Ⅰ)填充上表;
(Ⅱ)若以上表频率作为概率,且每天的销售量相互独立.
①5天中该种商品恰好有2天的销售量为1.5吨的概率;
②已知每吨该商品的销售利润为2千元, 表示该种商品两天销售利润的和(单位:
表示该种商品两天销售利润的和(单位:
千元),求 的分布列.
的分布列.
(本小题满分l2分)
已知△ABC的三个内角A,B,C所对的边分别为



 且
且
(Ⅰ)求 的大小;
的大小;
(Ⅱ)若
 求
求 △ABC。
△ABC。
(本小题满分14分

 )
)
设数列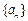 为等比数列,数列
为等比数列,数列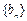 满足
满足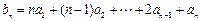 ,
,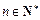 ,已知
,已知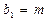 ,
,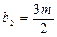 ,其中
,其中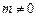 .
.
(Ⅰ) 求数列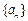 的首项和公比;
的首项和公比;
(Ⅱ)当m=1时,求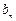 ;
;
(Ⅲ)设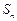 为数列
为数列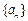 的前
的前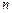 项和,若对于任意的正整数
项和,若对于任意的正整数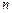 ,都有
,都有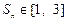 ,求实数
,求实数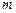 的取值范围.
的取值范围.