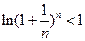(本小题满分12分)已知数列 的前
的前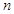 项和为
项和为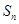 ,
,
(1)若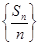 为等差数列,证明
为等差数列,证明 为等差数列;
为等差数列;
(2)在(1)的条件下,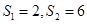 ,求数列
,求数列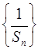 的前
的前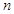 项和
项和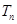 ;
;
(3)在(1)(2)的条件下,若存在实数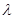 使得对一切
使得对一切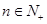 ,有
,有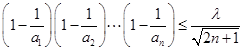 成立,求
成立,求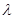 的最小值.
的最小值.
(本小题满分14分)已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若以函数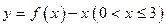 图像上任意一点
图像上任意一点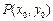 为切点的切线的斜率
为切点的切线的斜率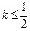 恒成立,求实数a的最小值;
恒成立,求实数a的最小值;
(本小题满分14分)如图,已知矩形ABCD的边AB="2" ,BC=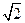 ,点E、F分别是边AB、CD的中点,沿AF、EC分别把三角形ADF和三角形EBC折起,使得点D和点B重合,记重合后的位置为点P。
,点E、F分别是边AB、CD的中点,沿AF、EC分别把三角形ADF和三角形EBC折起,使得点D和点B重合,记重合后的位置为点P。
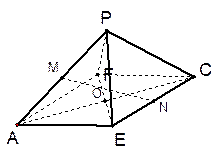
(1)求证:平面PCE 平面PCF;
平面PCF;
(2)设M、N分别为棱PA、EC的中点,求直线MN与平面PAE所成角的正弦;
(3)求二面角A-PE-C的大小。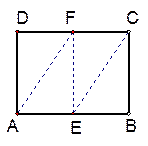
(本小题满分12分)某公司向市场投放三种新型产品,经调查发现第一种产品受欢迎的概率为 ,第二、第三种产品受欢迎的概率分别为
,第二、第三种产品受欢迎的概率分别为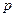 ,
, (
(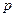 >
> ),且不同种产品是否受欢迎相互独立。记
),且不同种产品是否受欢迎相互独立。记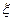 为公司向市场投放三种新型产品受欢迎的数量,其分布列为
为公司向市场投放三种新型产品受欢迎的数量,其分布列为
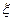 |
0 |
1 |
2 |
3 |
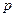 |
 |
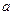 |
 |
 |
(1)求该公司至少有一种产品受欢迎的概率;
(2)求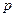 ,
, 的值;
的值;
(3)求数学期望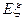 。
。
(本小题满分12分)设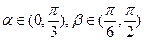 ,且
,且 满足
满足
(1)求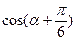 的值.(2)求
的值.(2)求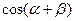 的值.
的值.
已知函数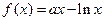 .(
.(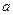 为常数)
为常数)
(1)当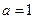 时,求函数
时,求函数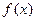 的最小值;
的最小值;
(2)求函数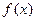 在
在 上的最值;
上的最值;
(3)试证明对任意的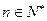 都有
都有