家政服务公司根据用户满意程度将本公司家政服务员分为两类,其中A类服务员12名,B类服务员 名
名
(1)若采用分层抽样的方法随机抽取20名家政服务员参加技术培训,抽取到B类服务员的人数是16, 求 的值
的值
(2)某客户来公司聘请2名家政服务员,但是由于公司人员安排已经接近饱和,只有3名A类家政服务员和2名B类家政服务员可供选择
①请列出该客户的所有可能选择的情况
②求该客户最终聘请的家政服务员中既有A类又有B类的概率
已知平面直角坐标系xOy,以O为极点,x轴的非负半轴为极轴建立极坐标系,P点的极坐标为 ,曲线C的极坐标方程为
,曲线C的极坐标方程为
(Ⅰ)写出点P的直角坐标及曲线C的普通方程;
(Ⅱ)若 为C上的动点,求
为C上的动点,求 中点
中点 到直线
到直线 (t为参数)距离的最小值
(t为参数)距离的最小值
如图所示, 为圆
为圆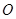 的切线,
的切线, 为切点,
为切点,
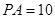 ,
,
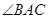 的角平分线与
的角平分线与 和圆
和圆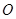 分别交于点
分别交于点 和
和
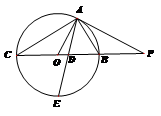
(1)求证 (2)求
(2)求 的值
的值
已知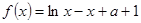
(1)若存在 使得
使得 ≥0成立,求
≥0成立,求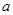 的范围
的范围
(2)求证:当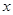 >1时,在(1)的条件下,
>1时,在(1)的条件下, 成立
成立
已知椭圆中心在原点,焦点在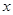 轴上,焦距为2,离心率为
轴上,焦距为2,离心率为
(1)求椭圆的方程;
(2)设直线 经过点
经过点 (0,1),且与椭圆交于
(0,1),且与椭圆交于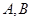 两点,若
两点,若 ,求直线
,求直线 的方程.
的方程.
已知梯形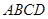 中
中 ,
,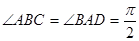 ,
,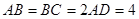 ,
,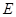 、
、 分别是
分别是 、
、 上的点,
上的点,
 ,
,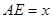 .沿
.沿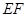 将梯形
将梯形 翻折,使平面
翻折,使平面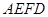 ⊥平面
⊥平面 (如图).
(如图).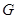 是
是 的中点.
的中点.
(1)当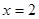 时,求证:
时,求证: ⊥
⊥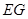 ;
;
(2)当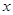 变化时,求三棱锥
变化时,求三棱锥 体积的最大值.
体积的最大值.