已知:如图1,平面直角坐标系 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐
标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线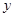 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
(1)在点D运动的过程中,若△ODE的面积为S,求S与 的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;
(2)如图2,当点E在线段OA上时,矩形OABC关于直线DE对称的图形为矩形O′A′B′C′,C′B′分别交CB,OA于点D,M,O′A′分别交CB,OA于点N,E.求证:四边形DMEN是菱形;
(3)问题(2)中的四边形DMEN中,ME的长为____________.

解方程组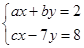 时,本应解出
时,本应解出
 ,由于看错了系数
,由于看错了系数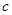 ,而得出解
,而得出解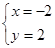 ,求
,求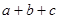 的值。
的值。
已知:如图AD∥BE,∠1=∠2,试说明:∠A=∠E.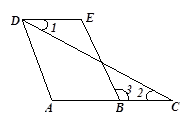
(1)如图(1)∠AOB和∠COD都是直角,请你指出∠AOD和∠BOC之间的数量关系;
(2)当∠COD绕点O旋转到如图(2)所示的位置时,上述结论还成立吗?请说明理由.
(3)如图(3),当∠AOB=∠COD=β(0°<β<90°)时,请你直接写出∠AOD和∠BOC之间的数量关系(不用说明理由).
王老师购买了一套经济适用房,她准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
(1)用含x的式子表示厨房的面积m2,卧室的面积m2;
(2)此经济适用房的总面积为m2;
(3)已知厨房面积比卫生间面积多2m2,且铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
先化简,再求值: .其中
.其中 .
.