如图：在正方形网格中有一个△ABC，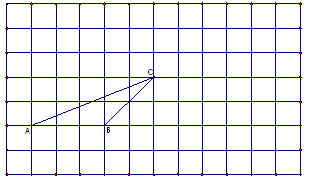
按要求进行下列作图（只能借助于网格）：
（1）画出△ABC中BC边上的中线（需写出结论）。
（2）画出先将△ABC向右平移6格，再向上平移3格后的△DEF。
（3）画一个锐角△MNP（要求各顶点在格点上），使其面积等于△ABC的面积。
阳光公司决定按左图给出的比例，从甲、乙、丙三个工厂共购买200件同种产品A，已知这三个工厂生产的产品A的优品率如下表所示．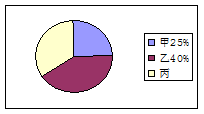
| 甲 |
乙 |
丙 |
|
| 优品率 |
80% |
85% |
90% |
⑴阳光公司从甲厂应购买件产品Ａ，从乙厂应购买件产品Ａ，从丙厂应购买件产品Ａ；
⑵阳光公司所购买的200件产品A的优品率为；
⑶你认为阳光公司能否通过调整从三个工厂所购买的产品A的比例（每个工厂的购买数均大于0），使所购买的200件产品A的优品率上升3%．若能，请问应从甲厂购买多少件产品A；若不能，请说明理由．
如图，在△ABC和△DEF中，AC∥DE，∠EFD与∠B互补，DE=mAC（m＞1）．试探索线
段EF与AB的数量关系，并证明你的结论．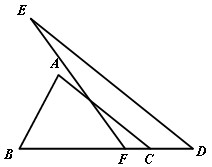
有3张不透明的卡片，除正面写有不同的数字外，其它均相同．将这三张卡片背面朝上洗匀后，第一次从中随机抽取一张，并把这张卡片标有的数字记作一次函数
中的k，第二次从余下的两张卡片中再随机抽取一张，上面标有的数字记作一次函数中的b．
（1）写出k为负数的概率；
（2）求一次函数y=kx+b的图象经过一、二、四象限的概率．（用树状图或列表法求解）
如图，一次函数y＝kx＋b与反比例函数y＝
的图象交于A（2，3），B（－3，n）两点．
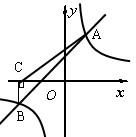
（1）求一次函数与反比例函数的解析式；
（2）根据所给条件，请直接写出不等式kx＋b＞的解集；
（3）过点B作BC⊥x轴，垂足为C，连接AC，求S△ABC．
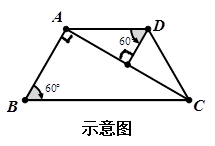
如图，在等腰梯形ABCD中，∠B=60º，且AB=AD=CD，请你将等腰梯形分成3个三角形，
使得其中有两个是相似三角形，且相似比不为1．
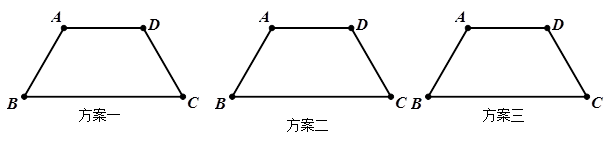
现在请你参考示意图，另外再给出三种分割方法（注：在两个相似三角形中标明必要的角度．）
