已知:如图,直径为OA的⊙M与x轴交于点O、A,点B、C把弧 CA分为三等份,连接MC并延长交y轴于点D(0,3)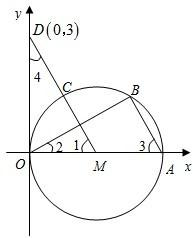
(1)求证:△OMD≌△BAO;
(2)若直线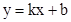 把⊙M的周长和△OMD面积均分为相等的两部份,求该直线的解析式.
把⊙M的周长和△OMD面积均分为相等的两部份,求该直线的解析式.
小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?
(成本=进价×销售量)
如图,直角三角形ABC中,∠C=90°,∠A=30°,点O在斜边AB上,半径为2的⊙O过点B,且切AC边于点D,交BC边于点E,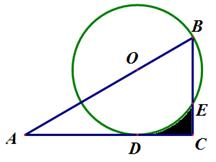
求:(1)弧DE的长; (结果保留π)
(2)由线段CD,CE及弧DE围成的阴影部分的面积。(结果保留π和根号)
抛物线y=-x2+(m-1)x+m与y轴交于点(0,3).
(1)求抛物线的解析式;
(2)求抛物线与x轴的交点坐标;
(3)画出这条抛物线大致图象;
(4)根据图象回答:
①当x取什么值时,y>0 ?
②当x取什么值时,y的值随x的增大而减小?
如图,已知反比例函数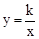 与一次函数
与一次函数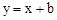 的图象在第一象限相交于点A(1,
的图象在第一象限相交于点A(1,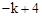 ),
),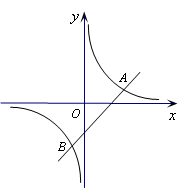
(1)试确定这两个函数的表达式;
(2)求出这两个函数图像的另一个交点B的坐标,并根据图象写出使一次函数的值小于反比例函数值的x的取值范围.