近期温州哄哄烈烈的展开了六城联创活动，抱着我为文明温州出一份力的想法，小华就公众对在餐厅吸烟的态度进行了随机抽样调查，主要有四种态度：
| A．顾客出面制止； | B．劝说进吸烟室； | C．餐厅老板出面制止； | D．无所谓．他将调查结果绘制了两幅不完整的统计图．请你根据图中的信息回答下列问题： |
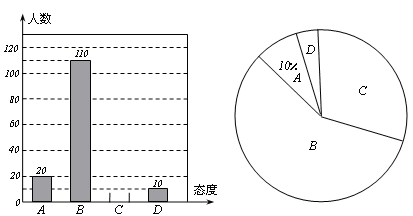
图① 图②
(1)这次抽样的公众有__________人；
(2)请将统计图①补充完整；
(3)在统计图②中，“无所谓”部分所对应的圆心角是多少度？
(4)若温州全市人口有800万人，估计赞成“餐厅老板出面制止”的有多少万人？并根据统计信息，谈谈自己的感想．(不超过30个字)
如图，已知D是AC上一点，AB=DA，DE∥AB，∠B=∠DAE。求证：BC=AE。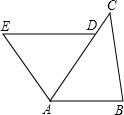
2011年3月10日12时58分，在云南盈江县发生5.8级地震，随后又相继发生里氏4.7级、里氏4.5级、里氏3.6级余震。灾情发生后，全国人民抗震救灾，众志成城。湖州市政府也筹集了抗震救灾物资共120吨准备运往灾区，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）
| 车型 |
甲 |
乙 |
丙 |
| 汽车运载量（吨/辆） |
5 |
8 |
10 |
| 汽车运费（元/辆） |
400 |
500 |
600 |
（1）若全部物资都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？
（2）为了节省运费，市政府打算用甲、乙、丙三种车型同时参与运送，已知它们的总车辆数为14辆，你能分别求出三种车型的车辆数吗？此时的运费又是多少元？
某家电商场计划用9万元从生产厂家购进50台电视机．已知该厂家生产3种不同型号的电视机，出厂价分别为A种每台1500元，B种每台2100元，C种每台2500元．
（1）若家电商场同时购进两种不同型号的电视机共50台，用去9万元，请你研究一下商场的进货方案；
（2）若商场销售一台A种电视机可获利150元，销售一台B种电视机可获利200元，销售一台C种电视机可获利250元，在同时购进两种不同型号的电视机方案中，为了使销售时获利最多，你选择哪种方案？
某汽车行驶时油箱中余油量Q（升）与行驶时间t（小时）的关系如下表：
（1）写出用行驶时间t表示余油量Q的代数式Q= ；
（2）当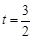
时，余油量Q的值为；
（3）汽车每小时行驶60公里，问油箱中原有汽油可供汽车行驶多少公里？
解不等式
，并将解集在数轴上表示出来，写出它的正整数解.