某家电商场计划用9万元从生产厂家购进50台电视机.已知该厂家生产3种不同型号的电视机,出厂价分别为A种每台1500元,B种每台2100元,C种每台2500元.
(1)若家电商场同时购进两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案;
(2)若商场销售一台A种电视机可获利150元,销售一台B种电视机可获利200元,销售一台C种电视机可获利250元,在同时购进两种不同型号的电视机方案中,为了使销售时获利最多,你选择哪种方案?
为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查,一测量船在 A岛测得 B岛在北偏西30°, C岛在北偏东15°,航行100海里到达 B岛,在 B岛测得 C岛在北偏东45°,求 B, C两岛及 A, C两岛的距离( 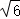 ≈2.45,结果保留到整数)
≈2.45,结果保留到整数)

下表是博文学校初三•一班慧慧、聪聪两名学生入学以来10次数学检测成绩(单位:分).
|
慧慧 |
116 |
124 |
130 |
126 |
121 |
127 |
126 |
122 |
125 |
123 |
|
聪聪 |
122 |
124 |
125 |
128 |
119 |
120 |
121 |
128 |
114 |
119 |
回答下列问题:
(1)分别求出慧慧和聪聪成绩的平均数;
(2)分别计算慧慧和聪聪两组数据的方差;
(3)根据(1)(2)你认为选谁参加全国数学竞赛更合适?并说明理由;
(4)由于初三•二班、初三•三班和初三•四班数学成绩相对薄弱,学校打算派慧慧和聪聪分别参加三个班的数学业余辅导活动,求两名学生分别在初三•二班和初三•三班的概率.
如图所示,抛物线 y= ax 2﹣  x+ c经过原点 O与点 A(6,0)两点,过点 A作 AC⊥ x轴,交直线 y=2 x﹣2于点 C,且直线 y=2 x﹣2与 x轴交于点 D.
x+ c经过原点 O与点 A(6,0)两点,过点 A作 AC⊥ x轴,交直线 y=2 x﹣2于点 C,且直线 y=2 x﹣2与 x轴交于点 D.
(1)求抛物线的解析式,并求出点 C和点 D的坐标;
(2)求点 A关于直线 y=2 x﹣2的对称点 A′的坐标,并判断点 A′是否在抛物线上,并说明理由;
(3)点 P( x, y)是抛物线上一动点,过点 P作 y轴的平行线,交线段 CA′于点 Q,设线段 PQ的长为 l,求 l与 x的函数关系式及 l的最大值.

如图,在△ ABC中,∠ C=90°,∠ ABC的平分线交 AC于点 E,过点 E作 BE的垂线交 AB于点 F,⊙ O是△ BEF的外接圆.
(1)求证: AC是⊙ O的切线;
(2)过点 E作 EH⊥ AB,垂足为 H,求证: CD= HF;
(3)若 CD=1, EH=3,求 BF及 AF长.

如图,一次函数 y= ax+ b的图象与反比例函数 y=  ( x>0)的图象交于点 P( m,4),与 x轴交于点 A(﹣3,0),与 y轴交于点 C, PB⊥ x轴于点 B,且 AC= BC.
( x>0)的图象交于点 P( m,4),与 x轴交于点 A(﹣3,0),与 y轴交于点 C, PB⊥ x轴于点 B,且 AC= BC.
(1)求反比例函数与一次函数的解析式;
(2)反比例函数图象上是否存在点 D,使四边形 BCPD为菱形?如果存在,求出点 D的坐标;如果不存在,说明理由.
